Experiments a l’Any Internacional de la Ciència i la Tecnologia Quàntica 2025 (IYQ2025).
Fa un parell d’anys vaig escriure una entrada, Experiències amb llum polaritzada: polaritzadors i retardadors, en la que explicava el fenomen de la polarització i mostrava experiments a portar a terme amb polaritzadors, però sempre des del punt de vista de la física clàssica.
En aquesta entrada també faré servir llum polaritzada però per il·lustrar alguns dels conceptes més interessants de la teoria quàntica, com són la superposició d’estats i com la mesura els afecta. Per això utilitzarem també aquí làmines polaritzadores com a polaritzadors, que com vam comentar son fàcils d’aconseguir i econòmiques (busqueu directament a google), i que com veurem es poden utilitzar per il·lustrar conceptes fonamentals de la mecànica quàntica.
La paradoxa dels tres polaritzadors
La paradoxa dels tres polaritzadors és un experiment magnífic, molt senzillet de fer però que dona molt de joc en explicar com es produeix per introduir algun dels conceptes clau de la física quàntica i, alhora, per veure la diferència amb la descripció que en fa la física clàssica.
Mira que havia vist la paradoxa amb tres polaritzadors i amb dos polaritzadors i un retardador al mig però mai havia caigut en lo paradoxal del fenomen, més aviat contraintuïtiu, fins que fa poc el vaig veure en un vídeo de youtube (el veureu més avall) que en feia referència i va ser quan em va xocar.
Recordem què és un Polaritzador. Des del punt de vista clàssic la llum (no polaritzada, la normal) és una ona electromagnètica en la que el camp elèctric i magnètic que la formen vibren en moltes direccions perpendicularment un a l’altre i en relació a la seva direcció de propagació. Un polaritzador és com una escletxa o una reixeta que només deixa passar les vibracions de la llum que estan alineades amb la reixeta, direcció que s’anomena eix de polarització.
Com vam veure a l’entrada que he comentat, la llum no polaritzada en passar per un polaritzador, per exemple vertical, només deixa passar la component vertical del camp i la intensitat es redueix a la meitat (50%). Si ara la llum polaritzada verticalment incideix sobre un altre polaritzador vertical, passarà tota (100%), però si incideix sobre un polaritzador horitzontal (a 90°), no passarà res (0%). Si el segon polaritzador es troba en un angle θ respecte a la polarització amb la que li arriba la llum, la intensitat transmesa tindrà un valor intermedi seguint la Llei de Malus: I=I0·cos2(θ)
L’experiment
Necessitem tres polaritzadors: P1, P2 i P3. Els podem subjectar amb la mà o ficar-los sobre la taula verticalment enganxats amb una agulla de roba o similar. La llum que farem passar pels polaritzador pot ser qualsevol: de la finestra, d’una bombeta, etc., sempre que no estigui ja polaritzada.

Col·locarem P1 amb el seu eix vertical (V, 0°) i P3 amb el seu eix horitzontal (H, 90°) després de P1, un davant de l’altre creuats. Si la llum no polaritzada incideix en P1 (vertical) surt polaritzada verticalment, amb intensitat I1 = I0/2. Aquesta llum vertical arriba després a P3 (horitzontal, 90° respecte a P1) i segons la Llei de Malus: I3 = I1·cos290° = I1·0 = 0. El resultat és que no passa llum.
Si ara fiquem P2 pel davant de P1 o bé darrere de P3 no es modifica la situació, continua sense passar llum sigui quina sigui la posició que adopti P2 (foto de dalt de l’esquerra), però si inserim P2 entre P1 i P3 amb el seu eix girat respecte a la vertical, sobre tot si és a 45°, torna apassar la llum pels tres polaritzadors (foto de dalt a la dreta). Mireu que xulo l’experiment en el vídeo que us deia abans:
Explicació de la paradoxa dels tres polaritzadors segons la Física Clàssica
Ens fixarem només en el camp elèctric E i deixarem de banda el camp magnètic associat B de la ona electromagnètica que és la llum que farem incidir en els polaritzadors.
Després de passar per P1 (0°) la llum estarà polaritzada verticalment. El seu camp elèctric E1 serà vertical i la seva intensitat serà I1 = I0/2, sent I0 la intensitat de la llum incident. Si a continuació la llum amb el camp elèctric vertical arriba a P2, que està a 45°, només deixarà passar la component del camp elèctric paral·lel al seu eix (45°), que ara sortirà polaritzada a 45°.
L’amplitud del camp que passa serà E2 = E1·cos(45°)
i la intensitat transmesa serà I2 = I1·cos2(45°) = I1 (1/√2)2 = I1/2
Per últim la llum polaritzada a 45° arriba a P3 que és un polaritzador horitzontal (90°), per tant, l’angle entre la polarització de la llum (45°) que li arriba i l’eix de P3 (90°) és també de 45°, i P3 només deixarà passar la component paral·lela al seu eix, com en el cas anterior.
L’amplitud que passarà serà E3 = E2·cos(45°)
I la intensitat transmesa serà I3 = I2·cos2(45°) = (I1/2) (1/√2)2 = (I1/2) (1/2) = I1/4
Globalment, doncs, la intensitat final de la llum que surt de P3 és I3 = (I0/2)/4 = I0/8.
Malgrat l’explicació, sembla estrany que per afegir un filtre (P2) entre dos filtres creuats (P1 i P3) que ja bloquejaven tota la llum, ara pugui passar una mica. L’explicació clàssica que hem vist és que en canviar P2 la direcció de polarització de la llum que el travessa, la llum que surt d’ell ja no és vertical sinó diagonal, i aquesta llum diagonal a la seva vegada té una component horitzontal que pot passar a través de P3. Funciona matemàticament amb la Llei de Malus, però segueix sent una mica xocant.
Explicació de la paradoxa dels tres polaritzadors segons la Mecànica Quàntica
La mecànica quàntica indica que la llum està composta per partícules quàntiques anomenades fotons i que la polarització és una propietat quàntica del fotó. Podem descriure els estats de polarització dels fotons usant vectors (kets en notació de Dirac), així:
Polarització vertical: |V⟩ o |0º⟩
Polarització horitzontal: |H⟩ o |90º⟩
Polarització diagonal a 45°: |D⟩ o |45º⟩
Aquests estats es relacionen. Per exemple, un estat diagonal és una superposició de vertical i horitzontal:
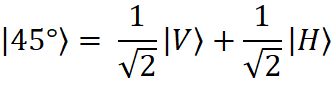
Això significa que un fotó polaritzat a 45° té un 50% de probabilitat de ser mesurat com a vertical i un 50% de ser mesurat com a horitzontal, i que un polaritzador actua com un aparell de mesura, de manera que quan un fotó interactua amb ell, o és absorbit (si la seva polarització és perpendicular a l’eix del polaritzador), o passa a través i, si ho fa, el seu estat de polarització col·lapsa a l’estat corresponent a l’eix del polaritzador.
Vegem ara què passa en el procés amb els tres polaritzadors: Els fotons que arriben a P1 (suposem que N fotons per segon) poden estar polaritzats en qualsevol direcció. Després de de passar per P1 (0°) els fotons estaran a l’estat |V⟩ i no hauran passat més que la mitat.
Cada fotó |V⟩ arriba a P2 (45°) interactua amb ell i P2 “pregunta” a cada fotó: ets |45°⟩?. La probabilitat que un fotó |V⟩ passi per un polaritzador a 45° és el quadrat de la “projecció” de |V⟩ sobre |45º⟩: (⟨45°|V⟩)2 = (1/√2)2 = 1/2
Ull! Els fotons que sí passen per P2, ara estan obligatòriament a l’estat |45º⟩ (el seu estat ha col·lapsat). És a dir, ara tenim N/4 fotons per segon a l’estat |45º⟩.
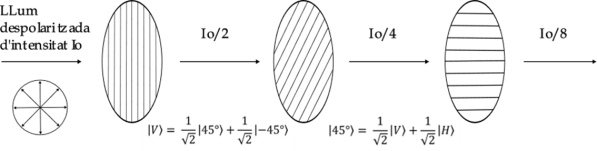
Aquests fotons que han passat per P2 arriben a P3 (horitzontal, (90°), |H⟩) en estat |45°⟩ i P3 “pregunta”: ets |H⟩?. L’amplitud de probabilitat és ⟨H|45°⟩ i per tant la probabilitat de passar és (⟨45°|V⟩)2 = (1/√2)2 = 1/2. Els fotons que han passat per P3 són a l’estat |H⟩ i en una quantitat N/2/2/2 = N/8.
Per tant, si la intensitat abans de P1 era I0, la intensitat final és I3 = I0/8, Que coincideix amb el resultat clàssic, encara que la mecànica quàntica explica el fenomen de forma més natural (😉) a través del concepte de mesura i col·lapse de l’estat quàntic.
La clau quàntica és que la mesura del segon polaritzador (P2) altera fonamentalment l’estat del sistema (el fotó), permetent un resultat que pot semblar impossible si pensàvem que el fotó recordava el seu estat original |V〉.
En resum, ambdues teories prediuen el mateix resultat observable (la intensitat final), però la interpretació subjacent de la física quàntica del que està passant (el col·lapse de l’estat del fotó) és radicalment diferent. Podeu aprofundir a l’article de The Chemical Educator (2002) Polarized Light and Quantum Mechanics: An Optical Analog of the Stern-Gerlach Experiment dels professors Joseph M. Brom i Frank Riouxá del departament de química de la Universitat de St. Thomas, Minnesota.
| Característica | Física Clàssica (Ona) | Mecànica Quàntica (Fotó) |
| Llum és… | Una onda electromagnètica continua | Partícules discretes (fotons) amb propietats quàntiques |
| Polarització | Direcció del vector camp elèctric E | Un estat quàntic del fotó |
| Polaritzador | Filtre que selecciona una component del E | Aparell de mesura que projecta/col·lapsa l’estat quàntic |
| Intensitat | Proporcional al quadrat de l’amplitud (E2) | Proporcional al número de fotons (o probabilitat) |
| Llei de Malus | I=I0cos2(θ) (projecció de vectors) | Probabilitat |
| “Paradoxa” explicada per | Canvi de la direcció de polarització de l’ona | Col·lapse de l’estat quàntic degut a la mesura intermèdia |
L’experiment de la doble escletxa amb llum polaritzada
Aquest experiment també és una demostració molt curiosa d’alguns dels conceptes més antiintuïtius i fonamentals de la mecànica quàntica com són la dualitat ona-partícula, la superposició d’estats, i com l’acte de mesurar o d’obtenir informació sobre un sistema quàntic n’afecta el comportament.
L’experiment bàsic de la doble escletxa (Sense Polaritzadors)
Ja hem vist en una entrada anterior, Experiments de difracció en escletxes i Principi d’incertesa de Heisenberg, el fenomen de la difracció i la interferència de la llum a través de dues escletxes en el que l’explicaven des del punt de vista de la física clàssica.
Si pensem en la llum d’un làser com una ona, quan arriba a les dues escletxes cada ranura actua com una nova font d’ones. Les ones que surten de cada escletxa s’expandeixen i se superposen a l’espai entre la barrera i la pantalla. On les crestes de les ones de les dues escletxes coincideixen, se sumen (interferència constructiva), creant una zona brillant a la pantalla. On la cresta d’una ona coincideix amb la vall de l’altra, es cancel·len (interferència destructiva), creant una zona fosca. El resultat a la pantalla és un patró d’interferència de franges brillants i fosques alternades, prova que va ser fonamental per establir el comportament ondulatori de la llum.
La física quàntica, però, ens diu que la llum està composta per partícules anomenades fotons. Si disparem els fotons del làser cap a les escletxes, sorprenentment cada fotó individual sembla passar per ambdues escletxes alhora, i tot i que cada fotó arriba a un punt concret de la pantalla (comportament de partícula), si esperem que arribin suficients fotons, el patró que formen junts continua sent el mateix patró d’interferència de franges brillants i fosques.
Això s’explica dient que cada fotó existeix en un estat de superposició, és a dir, la seva funció d’ona (el quadrat de la qual descriu la probabilitat de trobar-lo en un lloc) es propaga pels dos camins possibles (les dues escletxes) simultàniament.
La funció d’ona que passa per una escletxa interfereix quànticament amb la funció d’ona que passa per l’altra. El patró a la pantalla reflecteix la probabilitat resultant d’on és més probable que impacti el fotó (franges brillants) i on és menys probable (franges fosques). El fotó individual interfereix amb ell mateix. Tela! 😉.
Introduint els polaritzadors a l’experiment de la doble escletxa
Ara modifiquem l’experiment de la doble escletxa incorporant polaritzadors davant les ranures de manera que ens proporcionaran informació del camí que ha seguit el fotó ja que si està polaritzat per exemple verticalment sabrem per quina de les dues escletxes ha passat.

Col·loquem un polaritzador diferent sobre cada escletxa. Per exemple, un polaritzador vertical (V) a l’escletxa de la dreta i un polaritzador horitzontal (H) a l’escletxa de l’esquerra de la diapositiva. La llum que incideix inicialment no està polaritzada o està polaritzada de manera que pugui passar per tots dos (per exemple, a 45º).
En aquest moment el patró d’interferència desapareix. A la pantalla, en lloc de franges, veiem una distribució de llum més simple, bàsicament com si s’hagués esborronat el patró, sense les franges fines d’interferència (veure les fotos més a baix).
L’explicació de per què desapareix la interferència te en consideració que ara tenim informació del camí ja que ara els polaritzadors “marquen” els fotons. Si un fotó arriba a la pantalla i detectem que està polaritzat verticalment, sabem amb certesa que ha d’haver passat per l’escletxa de la dreta (la que tenia el polaritzador V). Si detectem que està polaritzat horitzontalment, sabem que va passar per l’escletxa de l’esquerra (la del polaritzador H).
En mecànica quàntica, l’acte d’obtenir informació sobre quin camí ha seguit la partícula (el que s’anomena which-path information o informació del camí) destrueix la superposició. En poder distingir quin camí va prendre el fotó, la seva funció d’ona “col·lapsa”. Ja no existeix com una ona que passa per les dues escletxes i interfereix amb si mateixa. Es comporta com una partícula que ha seguit un camí definit (el de l’esquerra o el de la dreta), i sense superposició no hi ha interferència.

Aquí ve per mi la part més curiosa. Si mantenim els polaritzadors V i H a les escletxes, però ara col·loquem un tercer polaritzador després de les escletxes (però abans de la pantalla) orientat en diagonal (D), per exemple a 45º respecte a la vertical i horitzontal, el resultat d’aquest canvi és que el patró de interferència reapareix, no ben bé com l’inicial sense polaritzadors, però reapareix!. Com és possible?
L’explicació quàntica és que el polaritzador diagonal esborra (esborrat quàntic) la informació del camí que havíem obtingut. Un fotó polaritzat verticalment (V) que ve de l’escletxa dreta té una certa probabilitat (50%) de passar a través del polaritzador diagonal (D), i si ho fa, sortirà polaritzat diagonalment. Un altre fotó ara polaritzat horitzontalment (H) que ve de l’escletxa esquerra també té una certa probabilitat (50%) de passar a través del polaritzador diagonal (D), i si ho fa, també sortirà polaritzat diagonalment.
Quan els fotons han passat pel polaritzador diagonal i arriben a la pantalla, tots estan polaritzats diagonalment (D). Ja no podem saber si originalment eren V (i van venir de l’escletxa dreta) o H (i van venir de la escletxa esquerra) només mirant la seva polarització final. La informació del camí ha estat esborrada.
En esborrar la informació que distingia els camins, restaurem la possibilitat de la superposició. Les components de la funció d’ona corresponents a cada camí tornen a ser indistingibles i, per tant, poden tornar a interferir, recreant el patró de franges a la pantalla (format només pels fotons que van aconseguir passar el polaritzador D). Guai, no?
La primera noticia de l’experiment amb polaritzadors ve de Rachel Hillmer i Paul Kwiat (2007), professors de la Universitat de Illinois, a l’article A Do‐It‐Yourself Quantum Eraser a l’extinta revista en Espanya Scientific American. Després Frank Rioux, professor del Departament de Química de la Universitat de Sant John’s (CSB|SJU) a Minnesota, a la publicació The Quantum Eraser ens proposa estudiar una demostració matemàtica del fenomen. Una alternativa és mirar aquest vídeo en el que es veu molt bé el muntatge casolà de l’experiment:
Una mica d’humor.

[…] Ja hem vist en entrades anteriors alguns experimentes que es poden realitzar amb làsers tals com: Mesura de la longitud d’ona d’un làser amb una xarxa de difracció, Mesura de l’amplada d’una escletxa o del gruix d’un cabell, o L’experiment de la doble escletxa amb llum polaritzada. […]
[…] és el dels tres polaritzadors que ja vaig explicar en una entrada anterior d’aquest bloc: Llum polaritzada i física quàntica. L’experiment clàssic és el de dues boletes en un pla inclinat, que és al que es refereix el […]