Després de tractar en diverses ocasions en aquest mateix bloc sobre la manera de mesurar la velocitat del so amb estudiants de secundària, tant a l’aire com en varetes metàl·liques, pot ser és el moment de fer una recopilació i curiosament (ohh!) han sortit 10 maneres de portar-ho a terme (bé, pot ser més).
Tantes formes d’abordar el problema comporten la possibilitat d’utilitzar diversitat de material i tecnologies, així com d’estudiar gran quantitat de conceptes relacionats amb les ones, el que resulta molt enriquidor.
- El valor de la velocitat del so a l’aire
- Aplicacions i material a utilitzar
- Mesura directa
- Mesura per eco
- Per formació d’ones estacionàries en un tub
- Petita historia de la mesura de la velocitat del so
El valor de la velocitat del so a l’aire
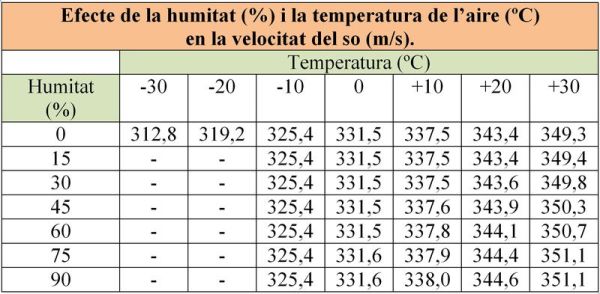
Actualment es considera que el valor de la velocitat del so a 0ºC a l’aire sec és de 331,45 m/s. La velocitat varia amb la humitat i la temperatura. Si només es té en consideració la temperatura es pot calcular la velocitat del so com:
Velocitat del so (m/s) = 331,4 + 0,6 t (si la temperatura està en graus centígrades)
Si es té en compte també la humitat, s’ha de considerar una taula com la de sota.
Aplicacions i material a utilitzar
Alguns dels procediments tenen a veure amb tecnologies clàssiques (regle i cronòmetre) i uns altres faran ús de les velles-noves tecnologies (ordinador i telèfon mòbil), per la qual cossa, al llarg de les diverses formes de realitzar les mesures haurem d’utilitzar també material, aplicacions i programari molt divers.
Aplicacions i programari
1 La primera aplicació que podem utilitzar serà el cronòmetre per mesurar el temps de vol del so (experiments 1 i 4). Tots els telèfons mòbils en tenen de sèrie una aplicació anomenada rellotge, alarma, despertador, o similar que incorpora al seu interior un cronòmetre.
2 Audacity. La primera interfície d’entrada de dades a l’ordinador és la de la tarja de so. Només amb aquesta i un micròfon barat ja es poden fer un munt d’experiències o de petites investigacions sobre el so aprofitant programes com Audacity (en aquesta entrada els experiments 2, 5 i 8). Fins i tot hi ha gent que (sense sobrepassar el 5 V d’entrada) la utilitza per connectar altres tipus de sensors. S’ha de parar compte amb la versió d’Audacity que es necessita ja que la versió 1.2.6 va ser l’última en la que es poden fer mesures en microsegons. Si no cal tanta precisió, o no us importa calcular els microsegons a partir del nombre de mostres i la freqüència a la que s’han obtingut, la versió actual ja us va bé. Un petit manual general.
3 Sempre va bé tenir instal·lades aplicacions de les denominades Suites que integren apartats per a obtenir dades de tots els sensors dels dispositius, com són Physics ToolBox Sensor Suite, o sobre tot en el cas que ens ocupa PhyPhox. Totes dues estan disponibles per Android i per iOS.
Com hi ha un parell de formes de mesurar la velocitat del so (la 3 i la 6) en les que és necessària l’aplicació PhyPhox, us hauríeu de decantar prioritàriament per aquesta.
4 Una altra aplicació a utilitzar és Ciencia Móvil – AudioTime+ (només per Android) que la utilitzarem per a mesurar el temps transcorregut entre dos sons (experiment 5). Tots els telèfons i tauletes tenen una aplicació que permet enregistrar veu, però no conec cap aplicació que, a més de fer això, permetin visualitzar el so i fer mesures (en microsegons) sobre la gràfica i manipular-la.
Sempre és possible guardar l’arxiu de veu amb una aplicació d’edició de veu i passar-lo a un ordinador per analitzar-lo amb Audacity, però amb AudioTime+ es podem fer aquestes accions en una tauleta (preferiblement, ja que la pantalla és més gran que en els telèfons i es poden ficar els dits més fàcilment) i, a més, gravar el so a través del micròfon del la pròpia tauleta o amb un micròfon extern connectat per l’entrada d’auriculars.
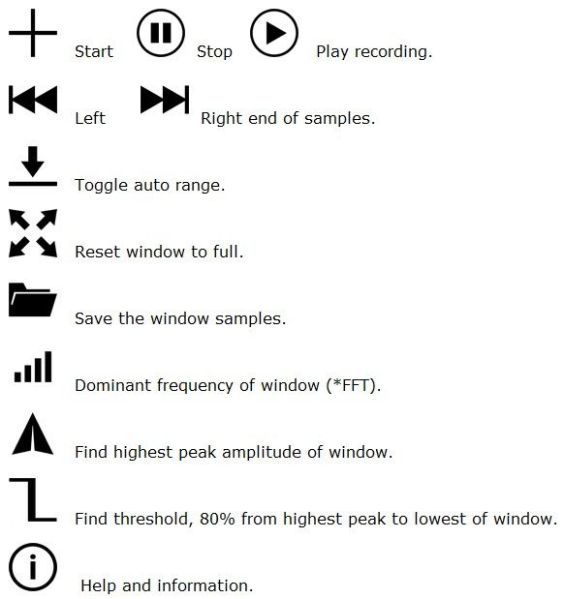
Bàsicament el funcionament de l’aplicació en la interacció amb la pantalla és:
- Tocant amb un dit la pantalla es marca una línia. Si a continuació es toca en un altre punt de la pantalla es visualitzen els registres en un interval de temps de color groc.
- Si s’arrossega una de les marques es modifica l’interval groc. Arrossegant amb dos dits alhora es pot fer zoom.
- Si es colpeja dues vegades la pantalla s’eliminen els marcadors de color groc.
I les funcions associades als botons són:
5 Hi ha desenes d’aplicacions que permeten generar un to d’una freqüència determinada. Es pot utilitzar qualsevol d’elles, però una que m’agrada molt és l’aplicació Function Generator que permet generar tons de la freqüència que interessi, bé introduint numèricament el valor o movent un cursor a dreta o esquerra per tal d’augmentar o disminuir la última freqüència. Aquesta aplicació de keuwlsoft té moltes més prestacions com pot ser la l’emetre la mateixa o una freqüència diferent per cadascú dels canals esquerre i dret, que per exemple es pot fer sevir per a produir batecs o per a experimentar amb interferències sonores. En la pàgina web dels autors troben un mini manual en anglès.
Ha estat elaborada per l’empresa Keuwlsoft, que té altres aplicacions com Spectrum Analyser (veure més endavant), totes de gran qualitat, gratuïtes, sense publicitat i que no demanen permisos.
Els que tingueu un iPhone o una iPad podeu fer servir l’aplicació Afinador de guitarra n-Track, que també està disponible per android.
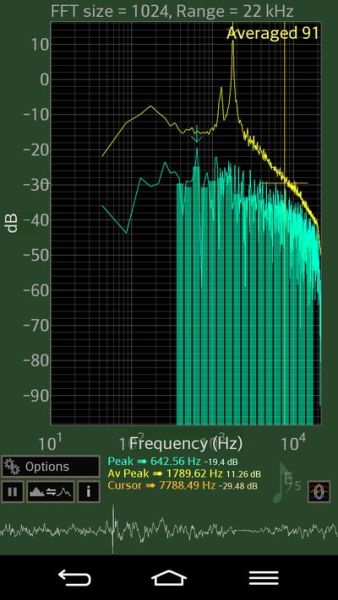
6 A més de generar tons, també hi ha casos en que es necessita obtenir la freqüència fonamental dels sons. La majoria de les aplicacions generals per enregistrar les dades obtingudes dels sensors dels telèfons (Suites) tenen un apartat que permet mesurar el to fonamental (pitch) d’un so. Però a l’experiment 8 us proposo una específica com és Spectrum Analyser. Analizador de sonido, que reté el valor de la última freqüència fonamental obtinguda i permet mirar-la amb tranquil·litat, a diferencia d’altres aplicacions que esborren el valor de la pantalla en pic que deixa de sentir-se el so.
7 Per trobar els diferents harmònics que poden sonar en un tub és molt útil l’aplicació Advanced Spectrum Analyzer PRO que, amb l’opció del menú Enable Peak Hold, reté l’últim anàlisi de fourier realitzat on es poden llegir els valors dels successius pics (experiment 9).
Material
El material més car que es necessita és un ordinador o un telèfon o tauleta, però afortunadament d’això anem tots sobrats 😉 . La resta de materials són tubs i micròfons que es poden aconseguir a un preu molt raonable. El llistat del material seria el següent:

- Cronòmetres pels experiments 1 i 4 (opcionals si no es disposa de telèfons mòbils)
- Dos tacs de fusta per xocar-los i fer soroll, pels mateixos experiments dels cronòmetres.
- Un ordinador va bé per a produir o gravar sons, per reproduir i analitzar vídeos i per connectar-li dataloggers amb els que adquirir les dades necessàries (experiments 1, 2, 5, 8, 10).
- Necessitarem un telèfon o una tauleta en la majoria d’experiments. Fins i tot en un cas seran necessaris dos telèfons (experiment 3).
- Una consola de recollida de dades (data-logger) com pot ser el Multilog o similar és opcional a l’experiment 2.
- Dos micròfons d’ordinador com aquest de la vora de PC Componentes.
- Tubs de cartró o PVC de qualsevol mida. Alguns d’ells s’haurien de poder empalmar per tal d’aconseguir arribar fins uns 3 m de longitud. Es poden comprar tubs de PVC a les botigues de fontaneria. Els tubs per guardar pòsters també van molt bé. Si no es disposa de tubs es poden fer enrotllant cartrons o cartolines que a la seva vegada es poden empalmar uns a continuació dels altres, el que permet aconseguir tenir tubs de longitud variable.
- En particular, per l’experiment 6 cal un tub de cartró, de paper o de plàstic que sigui prou gros per encabir dins el telèfon mòbil, i de la longitud que sigui.
- Als experiment 7 i 10 s’utilitza tub transparent. Els tubs transparents de plàstic (PVC) d’uns 4 cm de diàmetre es poden comprar a les ferreteries com el Servei Estació buscant tub rígid de PVC transparent.
- Si es vol construir un tub de Quincke (experiment 11) es necessiten tubs de plàstic, tes i colzes de dos gruixos diferents que encaixen un en l’altre.
- Tub d’assaig i flauta dolça (opcional) a l’experiment 8.
- Tub de Kund clàssic o modernitzat (opcional). En el seu defecte, un tub de plàstic (de PVC) transparent d’uns 4 cm de diàmetre i 80 cm de longitud i uns altaveus externs d’ordinador (experiment 10).
Mesura directa
1 El mètode del canó
Ara no el farem amb un canó, com al segle XVIII (veure la petita història), si més no utilitzarem dos tacos de fusta (o un petard) per a fer el soroll.
Una persona agafa un taco de fusta amb cada mà i, elevant-les per damunt del seu cap, les fa xocar procurant produir el soroll més gran possible (l’alternativa és que faci esclatar un petard dels de Sant Joan). Una altra persona es col·loca a 200 o 300 metres de distància amb un cronòmetre i mesura el temps entre l’instant en que veu el seu company o companya aixecar els braços fins que sent el soroll. La velocitat del so es calcularà com el quocient entre la distancia entre les dues persones i el temps mesurat: Vso = d/t
Aquest sistema te molts inconvenients, però també te l’avantatja de que conceptualment és el més comprensible i es pot utilitzar amb nens i nenes ben joves.
Per a minimitzar els errors s’han de fer les mesures en un dia serè sense vent i a la major distància possible mentre es continuï sentint el xoc de les fustes. Si es fa amb un grup d’alumnes estaria bé que varis d’ells prenguessin mesures alhora i que es tornés a fer l’experiència vàries vegades. Després es calcularia la mitjana i es rebutjarien les dades que marxessin més d’un 20 % (per exemple). Penseu que a una distància de 170 m el temps a mesurar és de l’ordre de 0,5 s, el que és molt poc.
Per a mesurar la distància entre els punts del terreny va bé una cinta mètrica llarga de les que usen a les classes d’educació física, i per a mesurar el temps poden utilitzar-se cronòmetres clàssics o bé l’aplicació cronòmetre que porten tots els telèfons mòbils.
Un mètode alternatiu per mesurar el temps consisteix en gravar l’experiència en vídeo, i després comptar els fotogrames i/o el temps que transcorre entre el fotograma amb el cop i en el que es sent el soroll enregistrat a la pista d’àudio.
2 Velocitat del so entre dos micròfons o auriculars
2.1 Velocitat del so entre dos micròfons i consola d’obtenció de dades
Si es disposa del maquinari adequat (ordinador i consola o interfície recol·lectora de dades) és possible també mesurar el temps que triga un so en recórrer la distància entre dos micròfons i calcular directament la velocitat. El so es pot fer amb un cop amb les mans, per exemple. La distància entre els micròfons dividida per la diferència de temps donarà la velocitat del so a la temperatura i humitat de l’habitació.
Velocitat del so = distancia entre micròfons/temps
S’ha de disposar de dos micròfons que es connecten a una consola de dades (data-logger) i aquesta a un ordinador. Si disposeu del Microlog ja tindreu també els dos micròfons. Si no disposeu de cap, es poden comprar els micròfons que venen per a endollar a un ordinador, que ja van prou bé i són barats. Consoles de recollida de dades hi ha de moltes categories i preus, però si no es disposa de consola per aquest motiu no recomano comprar cap. Com veurem més endavant podrem fer l’experiment amb altres alternatives.
Si es disposa de la consola d’obtenció de dades es connecten els micròfons en dos canals diferents i la consola a l’ordinador. Es fiquen els micròfons separats entre si una distància d’entre 1 i 3 m i en línia recta amb la producció del so, com s’indica en a l’equema de sota.
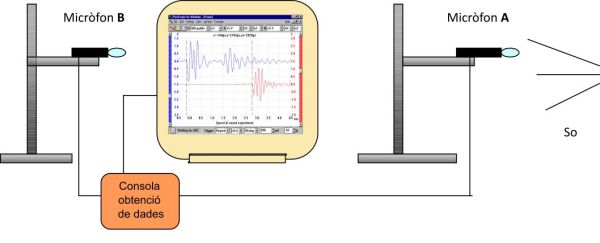
Es fica en marxa el programari que permet utilitzar la consola d’obtenció de dades (Multilab en el cas del Multilog) i es fa una forta picada de mans a una banda dels dos micros i en línia amb ells, s’atura la gravació i s’examina el gràfic que dona el mateix programari.
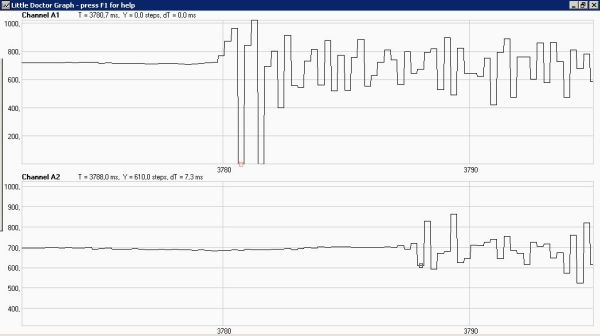
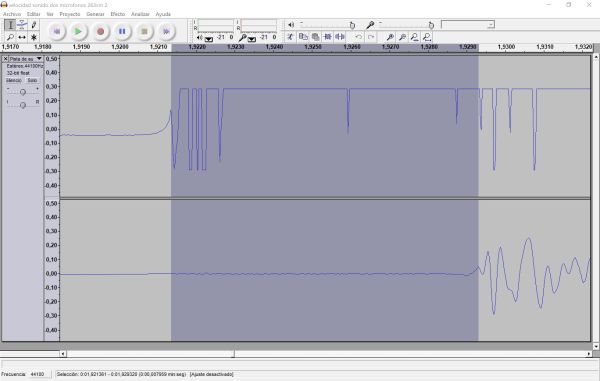
La pantalla mostrarà el registre del so que fa cada micròfon, com es veu, per exemple, en el gràfic de sota. Es mesura l’interval de temps entre l’inici dels sons en cada micròfon i es realitzen els càlculs.
Velocitat del so entre dos micròfons
Si no es disposa de consola es pot fer el mateix experiment amb dos micròfons connectats directament a l’entrada corresponent d’un ordinador que disposi d’entrada dedicada d’àudio (mic in). Prèviament els dos micròfons s’hauran de connectar directament entre si i utilitzar el programari Audacity (preferiblement la versió 1.2.6).
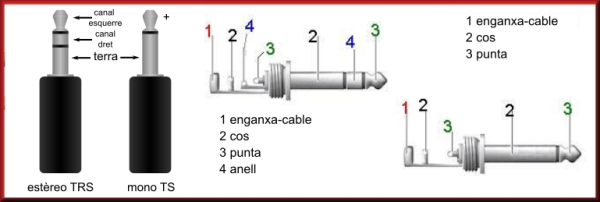
Els micròfons no s’han connectar entre si amb un adaptador com el de la fotografia de sota ja que encara que el mascle sigui estèreo (TRS, tres franges) les dues femelles estan connectades entre si i envien la mateixa senyal pels dos canals.

Es poden connectar manualment els dos micròfons entre sí, el que no és massa difícil però sí és laboriós ja que s’han de tallar els cables i soldar-los a un únic jack TRS. Qualsevol jack d’auriculars serveix, i sinó es pot comprar un. Es solden les dues masses dels dos micròfons juntes al cos (2), i l’altre cable de cada micròfon un a la punta (3) i l’altre a l’anell (4).
En tot cas el resultat pot ser com el de la pantalla de sota en la que el temps mesurat va ser de 0,0079 s. Com la distància entre micròfons era de 2,63 m, la velocitat del so resulta: Vso = 2,63/0,0079 = 332,9 m/s.
Velocitat del so entre dos auriculars
Però l’alternativa més fàcil i barata consisteix en connectar directament uns auriculars de tota la vida (com els de Renfe) a l’entrada del micròfon, tal i com l’explica James de Winter a la wiki Audacity Physics. Resulta que els auriculars funcionen també al revés fent de micròfons i com son estèreo ja venen amb un jack TRS de 3,5 en el que cada auricular ja està connectat a un canal. Encara que com a micròfons són un desastre al emetre una senyal molt baixa, per al nostre interès és suficient.
En qualsevol cas es connecten a l’entrada del micròfon de l’ordinador els dos micròfons o els dos auriculars separats el més possible entre sí per tal que la distància sigui el més gran possible i minimitzar errors, i s’obre el programa Audacity. Abans de gravar s’ha d’entrar en Editar – Preferències i en Gravació escollir dos canals (estèreo).
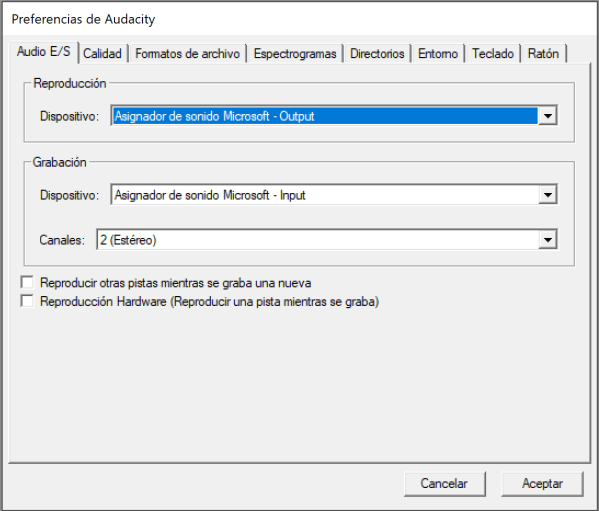
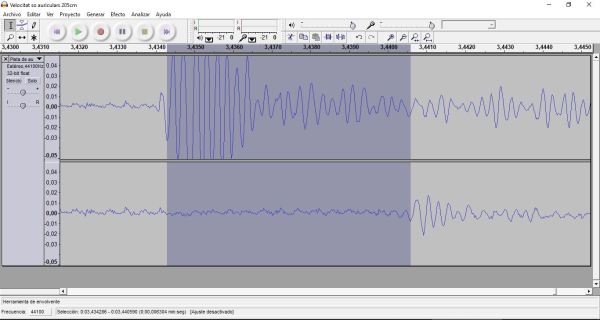
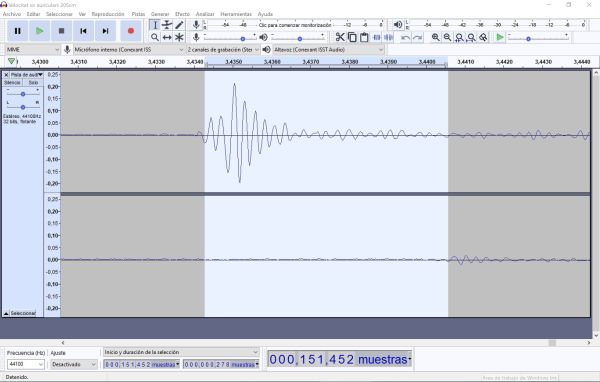
Ara no cal més que posar en marxa la gravació del programari Audacity i donar un cop a una banda dels auriculars i en línia amb ells, i ja es pot aturar la gravació. S’ha de seleccionar el boci on apareix el soroll gravat i ampliar-lo el més possible. Si es marca amb el ratolí el començament de les dues senyals en cadascú dels canals, directament el programa ens indica l’interval de temps a sota. Si amplieu la captura de pantalla veureu que marca 0,0063 s.
Si en lloc de la versió 1.2.6 d’Audacity useu l’actual, el programa no indica el temps fins a la milionèsima de segon, i el que s’ha de fer és demanar-li que indiqui la quantitat de mostres de l’interval per tal de dividir-lo per la freqüència a la que s’han fet les mesures, i que es mostra al costat. Si s’amplia la captura de pantalla es veu que indica 278 mostres i que la freqüència de mostreig ha estat de 44100 Hz. Ara es divideix el número de mostres per la freqüència i dona 0,0063 s.
Si es fan els càlculs amb les dades de l’experiment de les captures de pantalla de dalt, en el que la distancia entre auriculars va ser de 205 cm, es té:
Vso = 2,05/0,0063 = 325,4 m/s
El que és una bona aproximació a la velocitat del so, encara que millorable per altres mètodes de mesura.
Malauradament, molts ordinadors nous i els portàtils, telèfons i tauletes no disposen més que d’una única entrada i sortida d’àudio i graben només una pista. Per això en aquest cas, quan se connecten dos micròfons a un adaptador, interfície o jack, totes dues fonts es mesclen en una de sola en la gravació, i les dues pistes graven la mateixa senyal. Si que és veritat que s’aprecia la pujada del segon senyal del soroll del cop, però no amb suficient nitidesa com per a obtenir un bon valor per a la velocitat del so. Així que ja sabeu: al laboratori s’ha de disposar d’un ordinador de sobretaula o un portàtil que disposi de d’una entrada dedicada de micròfon (mic in, color rosa), i si és possible de micròfon i de línea (line in, blau).
3 Velocitat del so entre dos telèfons
Si es disposa de dos telèfons o tauletes és possible gracies a l’aplicació PhyPhox per a telèfons mòbils calcular la velocitat del so mesurant el temps que tarda en arribar un soroll d’un telèfon a un altre.
Per fer-ho es col·loquen dos telèfons sobre taules o al terra separats un de l’altre una distància prou gran per aconseguir valors de temps prou grans i minimitzar errors, però que es senti en un telèfon un soroll produït en la posició de l’altre. Entre 5 i 10 metres pot ser una bona distància.
S’inicia l’aplicació PhyPhox i l’apartat Conómetro acústico en els dos telèfons, es selecciona la mesura Simple. A continuació s’han d’introduir els valors Umbral i de Retraso mínimo per tal que els telèfons no es disparin pel soroll de fons o per ecos o reverberacions. Com es veu a les captures de pantalla de més avall un valor llindar de 0,3 o 0,4 i un de retard de 0,1 s són suficients si els estudiants no fan soroll mentre dura la pressa de dades.
Es fica en marxa l’aplicació als dos telèfons (no cal que sigui alhora) i una persona fa una picada de mans forta al costat d’un dels telèfons. A continuació una altra persona fa una altra picada de mans forta al costat de l’altre telèfon, i ja es poden aturar les aplicacions i veure el resultat. També pot fer l’experiment una única persona picant de mans en un telèfon i caminat fins l’altre per tornar a fer un soroll, però és més problemàtic perquè en el desplaçament es poden produir sorolls molt inconvenients
El resultat que he obtingut en col·locar els telèfons a 6 m de distància entre ells es mostra en les dues captures de pantalla de sota que corresponen als dos telèfons de l’experiment. El telèfon 1 és al mòbil en el que es va fer la primera picada de mans, i el telèfon 2 al de la segona.
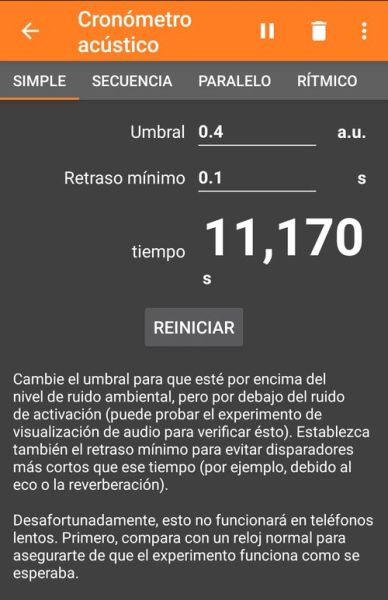
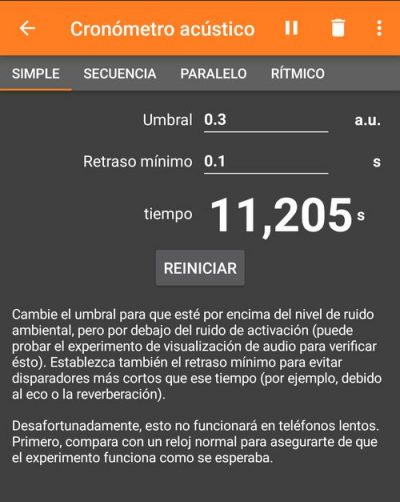
El temps 1 (t1) és el temps que mesura el telèfon on es dona la primera picada de mans i el temps 2 (t2) el temps que mesura l’altre telèfon. D’aquesta manera el càlcul de la velocitat del so es fa:

Que com es veu dóna estupendament.
Per a comprovar que la diferencia de temps dels dos telèfons correspon a dos vegades la distància entre ells s’ha d’entretenir un comprovant que la diferència de temps dels telèfons que s’aturen en sentir la segona picada de mans te a veure tant amb la distància que recorre el soroll en la primera picada, com després en la segona.
En el següent vídeo explica l’experiment el professor Sebastian Staacks, responsable de PhyPhox
Mesura per eco
Un segon grup de possibles formes de trobar la velocitat del so té a veure amb mesurar el temps d’anada i tornada d’un so quan es produeix el fenomen de l’eco. Aquest sistema te l’avantatja de no necessitar més que un micròfon, o només un telèfon.
4 Xocant dues fustes davant una paret
El mètode més simple és cronometrar un eco a oïda, però és difícil trobar una paret i una distància apropiades. En tot cas es pot mesurar aproximadament la velocitat del so de la següent manera:
Ens fiquem a uns 50 metres o més d’una paret (la distància mínima per sentir l’eco és d’uns 17 metres, 0,1 s) i una persona fa xocar dues fustes entre sí rítmicament intentant que el so de l’eco coincideixi amb el dels nostres cops (això es pot fer amb una mica d’entrenament). Una altra persona cronometra el temps en donar una quantitat elevada de xocs (20 cops, per exemple) i es divideix per aquesta quantitat. Es poden utilitzar cronòmetres de mà o l’aplicació cronòmetre que porten tots els telèfons.
El càlcul de la velocitat del so es realitza dividint el doble de la distància a la paret pel temps entre cops. Si es repeteix l’experiment vàries vegades i es calculen les mitjanes es troben resultats acceptables.
El més difícil de trobar és una paret adequada en un lloc amb poc soroll ambiental i un dia sense vent. Bruce Yeany ho aconsegueix en el vídeo de sota:
5 Amb un tub i un micròfon
Es pot fer el mateix experiment de la paret però en lloc de fer-ho a oïda, utilitzar un micròfon i gravar els sons d’anada i tornada per tal de mesurar en la pantalla de l’ordinador o la tauleta el temps transcorregut.
Amb ordinador i Audacity
Amb un ordinador i un micròfon, la mesura dels temps d’anada i tornada de l’eco és prou fàcil sempre que puguem aconseguir un tub una mica llarg per tal que el temps a mesurar no sigui massa petit. Un tub de plàstic (un tub de PVC de fontaneria) o de cartró d’uns 3 m de llarg i 4 o 5 cm de diàmetre està molt bé, encara que amb metre i mig ja n’hi ha prou.
Es fica el micròfon en una de les boques del tub, al que haurem tapat l’altre extrem. S’escull en Gravació, d’Editar – Preferències, gravar només un canal, i es comença la gravació. Es fa una picada de mans (o un cop amb unes castanyetes) a la boca del tub on és el micròfon, i s’atura la gravació.
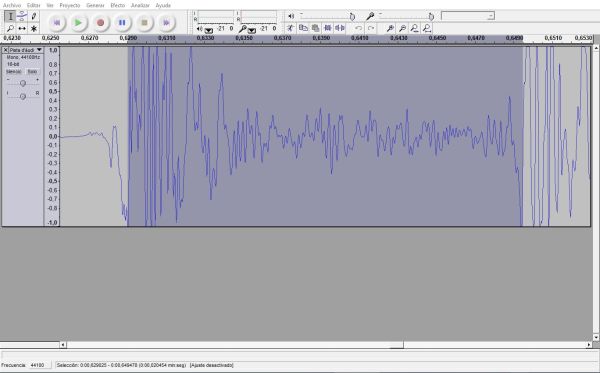
El resultat que s’obté és com el de la captura de pantalla de sota on per una longitud del tub de 3,47 m s’obté un temps d’anada i tornada del soroll 0,020 s.
D’aquesta manera ho fan els alumnes de Francisco Sotres i ho mostren en el següent vídeo:
Amb Tauleta i Audiotime+
Per a fer el mateix experiment amb Audiotime+ es necessita un tub com el del cas anterior i un telèfon o tauleta amb sortida d’auriculars on endollar un micròfon, com es veu a la fotografia.
El micròfon es col·loca a la boca del tub, que ha d’estar tancat per l’altre extrem. Normalment no es grava bé l’eco si directament es fica a la boca del tub el micròfon del telèfon o tauleta. Un micròfon qualsevol com el que es veu a la fotografia dona molts millors resultats i és prou barat.
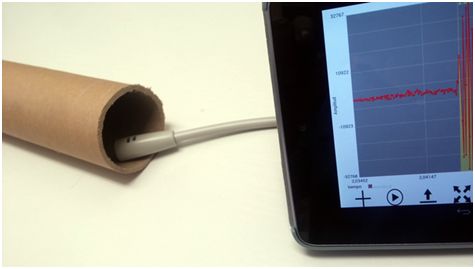
L’aplicació a utilitzar ha de ser capaç de gravar el so i després mostrar la gràfica de la seva intensitat en funció del temps per tal que sigui possible el mesurar l’interval de temps que passa entre dos sorolls. L’app Audiotime+ ho fa molt bé i és la que he utilitzat en aquest cas.
S’obre l’aplicació i es comença la gravació polsant el botó +. A continuació es fa una palmadeta amb les mans a la boca del tub i s’atura la gravació. El resultat és com es veu a la imatge de sota una vegada que s’ha engrandit la gràfica i s’ha marcat el principi del soroll i l’inici del seu eco pitjant successivament amb un dit en la pantalla. Les dues marques indiquen el temps en cada instant i a sota es mostra també el valor de l’interval.

En aquest cas l’experiment està fet amb un tub de cartró curt d’1,66 m de longitud, estant el temps d’anada i tornada del so dins el tub de 0,00974 s. Malgrat la curta longitud del tub el resultat per a la velocitat del so surt prou bé:
Vso = d/t = 2×1,66/0,00974 = 341 m/s
6 Amb un tub i un telèfon i PhyPhox
Continuant amb la mesura de la velocitat del so gràcies a l’eco us proposo aprofitar l’apartat Sonar de l’app PhyPhox que directament ja indica la velocitat del so que rebota en una paret, coneguda la distància a la que es fica el telèfon. L’app ho fa tot, no cal fer cap soroll ja que la mateixa aplicació emet el so que ha d’anar i tornar.
El professor Sebastian Staacks explica com fa l’experiència en el vídeo de sota. Jo l’he repetida i no surt massa bé, i si no s’aïlla bé el telèfon no hi ha manera d’aconseguir un resultat acceptable perquè el so s’escampa per tota la habitació i el mòbil rep ecos de tot arreu.

L’alternativa que proposo per a fer l’experiment és introduir el telèfon en un tub, de manera que el so no te més nassos que viatjar al seu llarg. Com he comentat en parlar del material qualsevol tub va bé, sempre que es pugui ficar el telèfon dins. El tub que he utilitzat per obtenir les dades que indico més avall es mostra en les fotografies i l’he fet d’una longitud d’1,69 cm amb el cartró d’una caixa.
S’ha de ficar el telèfon dins el tub en un dels extrems amb la part de sota cap a dins i la part de dalt cap enfora del tub, ja que en la majoria dels mòbils tant l’altaveu que emet el so, com el micròfon que el recull es troben en la base del telèfon.

L’altre extrem del tub, o bé es tapa, o bé es recolza sobre una paret en la que es reflectirà el so. Com que el telèfon que vaig utilitzar te una llargària de 15 cm, una vegada introduït en el tub la distància de l’altaveu i el micròfon a la paret va ser de 154 cm.
S’obre l’aplicació PhyPhox i dins l’apartat Sónar de l’Acústica s’escull Velocidad del sonido. S’inicia la pressa de dades i després de sentir dos o tres polsos de so s’atura l’app.
Si resulta incòmode fer l’operació directament sobre el telèfon sempre es pot usar l’accés remot amb un ordinador o un altre telèfon o tauleta. Per tal de enllaçar els dos aparells, abans d’introduir el telèfon en el tub, es premen els tres puntets de dalt a la dreta i es marca Permitir acceso remoto. Ara no hi ha més que enllaçar en el navegador de l’altre aparell a l’adreça IP que ha subministrat el mòbil, i ja apareix el duplicat de la pantalla de l’aplicació i es pot realitzar l’experiment a distància (han de ser els dos aparells a la mateixa xarxa wifi).

El resultat que s’obté es veu en la primera captura de pantalla de sota. Si es prem el símbol ampliar les gràfiques ocupen tota la pantalla i és possible ampliar-les i seleccionar dades i intervals entre les dades, com es mostra a les altres dos captures de sota, on s’obté un valor de 347 m/s per a la velocitat del so en mesura directa sense normalitzar.
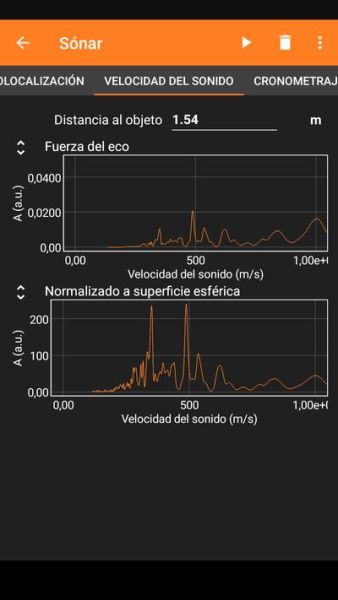
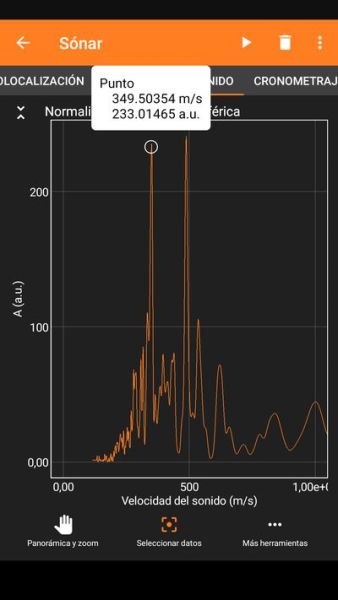
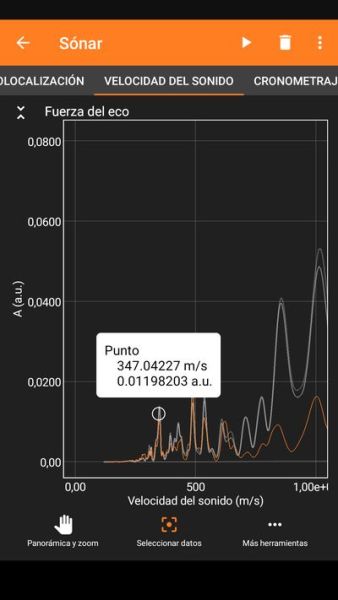
Si en lloc de voler mesurar la velocitat del so el que es vol es utilitzar l’app com a telèmetre, el que s’ha de fer és escollir Ecolocalización dins l’apartar Sónar i introduir un valor per a la velocitat del so.
Per formació d’ones estacionàries en un tub
7 Per ressonància en un tub submergit més o menys en aigua
El mètode de laboratori més clàssic és mitjançant la ressonància d’un tub transparent parcialment submergit en aigua, amb un diapasó, que és el que proposa aquest protocol del CDEC i es pot veure en aquest vídeo:
És un experiment que tradicionalment es realitzava als laboratoris de física utilitzant un diapasó, preferiblement d‘una freqüència més elevada (1000 Hz) que les que anaven en els equips ENOSA, que eren de 440 Hz, i un tub gros de vidre o plàstic connectat per la base a un embut gros.
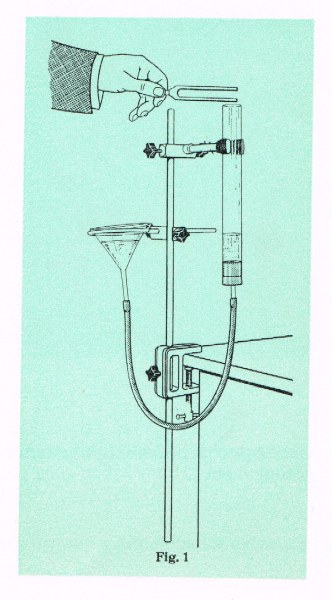
S’omplia el tub amb aigua fins a una altura a la boca del tub de 20 a 30 cm. Es copejava el diapasó i es ficava a la boca del tub. S’aixeca o baixa l’embut per a pujar o baixar l’altura de l’aigua al tub per l’efecte dels vasos comunicants fins que en un moment donat el tub ressona amb la freqüència del diapasó o un dels seus harmònics. Es mesura l’altura del tub lliure d’aigua i es passa a fer els càlculs.
A mi m’agrada més l’alternativa d’introduir tubs de plàstic d’uns 4 cm de diàmetre (de canonada, per exemple) i de diferents longituds dins una botella de plàstic transparent d’un litre o litre i mig tallada per la boca i plena d’aigua. El tub es baixa o puja fins que ressona i en aquest moment es mesura l’altura del tub que sobresurt de l’aigua.
En aquests moments, però, no necessitem diapasó. Amb un telèfon i l’app corresponent podem produir el to de la freqüència que vulguem i no és necessari moure res. N’hi ha prou amb mantenir el tub submergit a l’aigua i, amb l’altaveu del telèfon o tauleta a la seva boca, fer variar la freqüència fins que el tub ressoni. No necessàriament serà la freqüència fonamental, així que ara s’haurà de pujar o baixar el tub per a trobar les altres alçades a les que també ressona.
Els telèfons i tauletes tenen uns altaveus de poca potència. Si es vol que el tub ressoni fort i sigui més espectacular, s’ha d’utilitzar un tub gros, per exemple el d’una canonada de desaigüe d’uns 12 cm de diàmetre i un altaveu connectat al telèfon (per cable o per bluetooth), que és el que es ficarà a la boca del tub.
Un altre motiu que fa convenient usar altaveus externs al telèfon és que seran capaços de reproduir sons de freqüències baixes mentre que els altaveus dels mòbils moltes vegades ja no reprodueixen els tons per sota de 150 Hz.
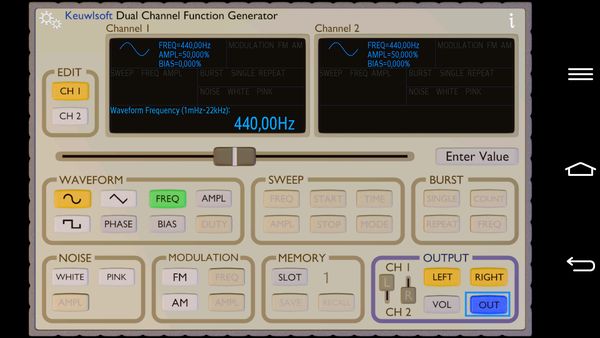
L’aplicació escollida per aquest cas és la estupenda Function Generator, però qualsevol suite (Physics ToolBox, per exemple) en té un apartat que permet generar la freqüència que interessi. Per a l’escombrada de freqüències s’han de marcar els quadrets que apareixen remarcats en la imatge de dalt de l’app Function Generator i arrossegar amb el dit el cursor a dreta o esquerra per tal de pujar o baixar la freqüència del to emès. Quan més es desplaci el cursor més ràpidament canviarà el valor.
Sigui com sigui, si hem aconseguit fer ressonar el tub amb l’harmònic fonamental, calcularem la velocitat del so en el tub com farem després en el cas del tub d’assaig: la velocitat del so serà igual al producte de la freqüència per quatre vegades l’altura del tub sense aigua.
Vso (aire) = f x λ = f x 4L
Per a fer-se una idea de les longituds lliures del tub per a que ressoni hem de considerar que amb una freqüència de 500 Hz el primer harmònic apareixerà a una altura del nivell d’aigua sobre la boca de menys de 17 cm i si la freqüència és de 1000 Hz la profunditat del tub buit serà de menys de 9 cm.
8 Tub d’assaig o flauta dolça
Si es disposa d’un ordinador, la forma més fàcil actualment de mesurar la velocitat del so en l’aire és gravant el so d’un tub d’assaig al que es bufa o d’una flauta dolça i analitzant la gravació amb un programari com Audacity.
Si bufem en la boca d’un tub, per exemple d’un tub d’assaig, podem aconseguir que ressoni i es produeixi un so que de vegades és una nota musical estàndard. En tot cas, gairebé mai és un so pur d’una única freqüència. En tots els instruments musicals passa una cosa similar: els sons que es produeixen són una barreja d’harmònics i altres freqüències que sentim totes alhora.
Els ordinadors, tauletes i telèfons tenen la capacitat de processar gran quantitat d’informació ràpidament i, amb l’ajut del programari o aplicació corresponent, d’analitzar les freqüències que es combinen en qualsevol so en realitzar el que es coneix com un anàlisi de Fourier i aportar el valor de la freqüència fonamental del to i, en alguns casos, dels seus harmònics successius.
Per a fer la mesura de la freqüència es bufa en la boca d’un tub d’assaig fins aconseguir produir un so musical mentre està gravant l’Audacity o es té en funcionament en el telèfon mòbil una aplicació com Spectrum Analyzer (o qualsevol suite a l’apartat d’anàlisi de so) que processa el so i indica directament la freqüència del seu harmònic fonamental.
L’experiment es pot repetir amb tubs d’assaig de diferent longitud, però si es realitza amb una flauta dolça es té l’avantatja que només tapant més o menys forats (les diferents notes de l’instrument) ja aconseguim tenir un tub de diferent mida, obert pels dos extrems en aquest cas.
Així com en Audacity una vegada gravat el so s’ha d’anar a Analitzar-Dibuixar espectre per veure la freqüència fonamental del so, a les aplicacions dels mòbils (com Spectrum Analyzer) a més de mostrar en temps real la gràfica de la descomposició del so, es mostra directament el valor de la freqüència fonamental en cada moment (Peak) en verd, la freqüència on es troba el cursor (Cursor) en marró i la mitjana de les últimes freqüències fonamentals (Av Peak) en groc. D’aquesta manera, encara que ja no soni el to a analitzar, es manté en pantalla la mesura que ens interessa. Si aquest valor no es mostra en la pantalla, s’ha anar a les opcions i en l’apartat Averaging ficar on. Per a resetejar els valors s’ha de pitjar en el 0 requadrat a sota a la dreta en la pantalla (mireu la imatge del costat).
Amb el valor de la freqüència fonamental ja només necessitem mesurar la llargària del tub d’assaig amb una regla mil·limetrada. S’ha de mesurar des de la base del tub (per fora) fins a la boca. Quan es forma l’ona sonora dins el tub, de fet, surt una mica de la seva boca, 0,6 vegades el radi, però com el cul dels tubs d’assaig és rodó i té un cert gruix, en mesurar de la manera que indico ja estem afegint el suplement.
La velocitat del so en l’interior del tub es calcula directament multiplicant la freqüència obtinguda per la longitud d’ona del to fonamental que es pot produir en l’interior d’un tub obert per un extrem (quatre vegades la seva longitud):
Vso (aire) = f x λ = f x 4L
Per explicar d’on surt la formuleta de dalt hem de considerar que en el cas d’un tub obert per un extrem, quan es formen ones estacionaries en el seu interior sempre en l’extrem tancat es forma un node i en l’obert un ventre, per tant l’ona mínima que se pot formar (primer harmònic, freqüència fonamental) correspon a un quart d’ona, i la seva longitud d’ona, λ, serà igual a quatre vegades la longitud del tub (de fet una mica més, com ja he indicat). El segon harmònic es forma quan s’encabeix tres quarts d’ona en el tub, en el tercer harmònic ha de ser una ona sencera i un quart, i així successivament.
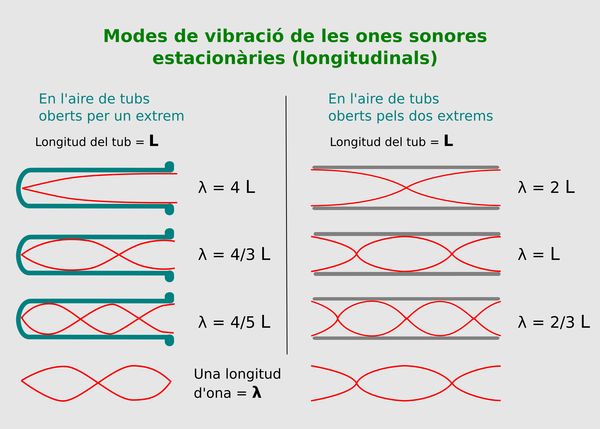
Malgrat que la representació de les ones sonores a les il·lustracions es visualitzi moltes vegades amb dibuixos transversals, com he fet en els de dalt per tal de veure millor les dimensions de les ones formades, s’ha de recordar que les ones sonores són longitudinals (són ones de pressió).
Per altra banda, la velocitat del so que s’obté variarà en funció de la temperatura i la humitat de l’aire dins el tub d’assaig. Com fem sonar el tub amb el nostre alè sempre tindrà més humitat i temperatura que l’aire circumdant (veure la taula del principi de l’entrada).
9 La velocitat del so per ressonància en un tub copejat, i mòbil
Dins l’apartat de ressonància proposo ara un experiment encara més casolà, però no per això menys rigorós: mesurar la velocitat del so en un tub de cartró en el que ressona un cop. Servirà qualsevol tub però quan més gran sigui millor, ja que sentirem els sons més alts quan ressoni. Un tub d’aquells en els que envien pòsters és ideal.
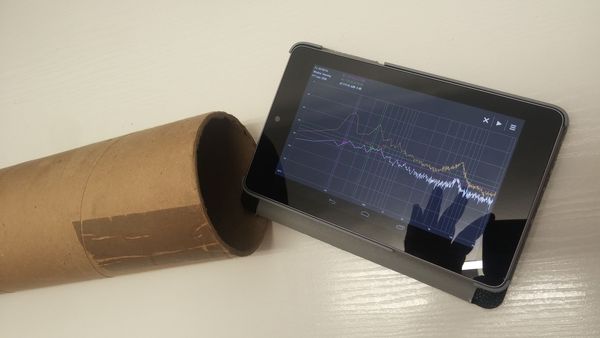
També necessitarem una aplicació al mòbil o tauleta que sigui capaç de donar els valors dels diferents harmònics que es formen al tub quan produïm un soroll al seu interior. L’aplicació Advanced Spectrum Analyzer PRO, que hem presentat al començament és estupenda. Les profesores Chantal i Ferrer ho fan amb Audacity i tubs de diferent longitud.
Obrirem l’app i l’indicarem que recordi l’últim anàlisi de fourier realitzat amb l’opció del menú Enable Peak Hold. Posarem el telèfon o la tauleta amb el micròfon en la boca del tub i li donarem uns copets al tub per a que soni. A continuació no cal més que mirar la gràfica que ens subministra l’aparell mòbil i apuntar els valors dels successius pics que corresponen a les freqüències dels diferents harmònics que ha estat capaç d’encabir el tub. Ha de sortir una gràfica com la de sota.
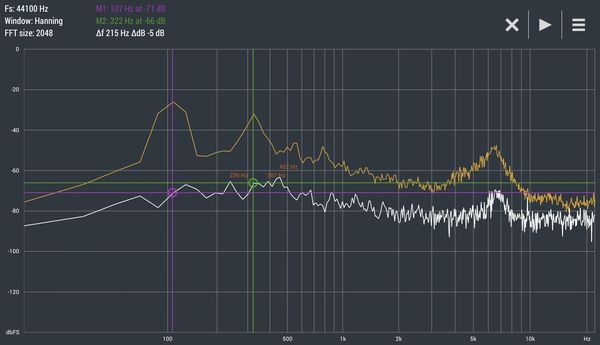
Per esbrinar el valor dels pics més significatius només cal pitjar la pantalla i arrossegar amb el dit la línia verda o violada que apareix fins als vèrtexs de la línia groga, de manera que els valors es mostren a dalt amb el mateix color de la línia corresponent. La gràfica de la figura s’ha obtingut copejant un tub de 74 cm de llarg i 9,5 cm de diàmetre amb un extrem tancat. El valor del primer harmònic és de 107 Hz i el del segon de 322 Hz. Si fem els càlculs:
Vso (primer harmonic) = λ x f = [4 x (74 + 4,75×0,6)] x 107 = 330 m/s
Vso (segon harmonic) = λ x f = [4/3 x (74 + 4,75×0,6)] x 322 = 330 m/s
Quan s’emet un so d’una determinada freqüència en la boca oberta d’un tub tancat per l’altre extrem, el so produït entra al tub comprimint l’aire en el seu interior i produint un tren d’ones que es reflecteix en arribar a l’extrem tancat del tub amb un canvi de fase de 180º. Resulta així, a l’interior del tub, una combinació d’ones incidents i reflectides que, per a determinades longituds del tub, produeixen ones estacionàries, amb un node a l’extrem tancat i un ventre, o amplitud màxima, una mica sortit de l’extrem obert del tub (mireu la gràfica de sota). El tub entra llavors en ressonància i es produeix una intensificació considerable del so emès.

La posició del primer ventre no coincideix exactament amb l’extrem obert del tub de ressonància, sinó que està fora d’ell, a una distància (d) igual a aproximadament 0.6 vegades el radi del tub. Així, tal i com s’ha considerat en els càlculs de dalt, la longitud del tub per la qual es produeixen les diferents ressonàncies ve determinada per l’expressió següent, on n = 1, 2, 3, …
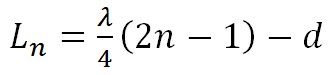
Per tal d’evitar l’inconvenient del paràmetre d en l’equació de dalt, a l’hora de calcular la longitud d’ona es pot determinar la longitud del tub lliure per a dues ressonàncies consecutives Ln i Ln+1, i la seva diferència correspondrà a mitja longitud d’ona, el que és independent de la posició del ventre a la boca del tub, per tant:
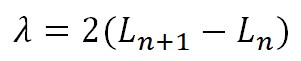
En el cas de que tinguéssim un tub obert per tots dos cantons les ones estacionàries que es formen en el tub tenen ventres als dos extrems, de manera que la longitud del tub per a la qual es produeixen les diferents ressonàncies ve donat per l’equació següent, On n = 1, 2, 3, …
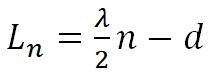
on el paràmetre d representa el que surt l’ona estacionària pels extrems del tub. Igual que en cas del tub tancat per determinar la longitud d’ona es pot restar la longitud de dues ressonàncies consecutives.
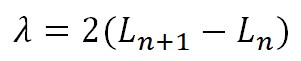
10 Tub de Kundt
Tub de Kundt clàssic
Els experiments relacionats amb el tub de Kundt també han estat tradicionals als laboratoris escolars ja que permeten mesurar la velocitat del so en diferents gasos (per exemple en butà) però necessitaven un utillatge més sofisticat que un diapasó: tenir el mateix tub de Kundt clàssic (veure l’explicació d’Ángel Franco en el seu Curs de Física interactiva en Internet) o un tub transparent de vidre o plàstic més un generador de funcions amb un amplificador i un altaveu, com es proposa en aquest protocol del CDEC.

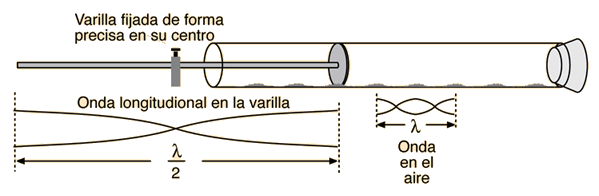
Per a produir el so que fes vibrar l’aire dins el tub i alhora les serradures de fusta, s’ha de fer vibrar la vareta metàllica parcialment introduïda en el tub. La vareta es subjecta pel seu centre i se la fa vibrar fregant-la amb la mà o un drap impregnats amb una mica de colofònia (resina per a violí) com fa Russell Clark en el vídeo de sota.
Tub de Kundt. Quan el generador de funcions és un telèfon mòbil
La versió més moderna, però que ja té uns quanta anys, del tub de Kund és la proposada pel protocol del CDEC (d’abans de 2002) en la que la vibració del gas contingut al tub és produïda per un altaveu acoblat en un extrem que emet un so d’una freqüència determinada i que és generat per un generador de funcions, com el seu nom indica.

En aquests moments, però, és possible realitzar l’experiment proposat pel CDEC reemplaçant el generador de funcions per un telèfon o tauleta, i l’amplificador i altaveu per uns altaveus d’ordinador (per exemple un altaveu bluetooth), de manera que ara el més difícil d’aconseguir és el tub i les serradures de suro.
L’aplicació a córrer en el telèfon serà qualsevol de les que ja hem utilitzat per a produir sons de la freqüència desitjada, com Function Generator, per exemple.
Altres tubs de Kundt
Recentment, César Sancho ha publicat un vídeo amb 3 Experiencias de ondas en tubos en una de les quals ens mostra un tub de Kund casolà que amb un xiulet funciona de meravella.
11 El tub de Quincke
De propina us proposo una altre manera de mesurar la velocitat del so per interferències sonores amb el tub de Quincke. Jo, ni l’e fet servir ni he construït un, però tot arribarà.
Angel Franco ens explica com funciona el tub de Quincke i inclou una simulació per a que practiquem, i Jorge Barrio, en una de les seves Clases de Física en Youtube en fa l’experiment a partir del minut 16:53.
Petita historia de la mesura de la velocitat del so
Per acabar aquesta entrada fico quatre notes sobre la historia de la mesura de la velocitat del so. Les notes es basen en publicacions ben diverses a les que us adreço si voleu aprofundir, com són els apartats de les wikipèdies en francès i anglès, el capítol sobre la velocitat del so del volum El sonido de El mundo físico del divulgador científic Amédée Guillemin (1882), l’entrada de Felipe González en el bloc idoneos, o l’article de Lindsay Hannah en la revista New Zealand Acoustics (2006). Pot ser aquest últim article ja seria suficient, encara que la lectura de El Mundo Físico crec que és interessantíssima.
Des de l’Antiguitat s’ha entès que el so es es propaga en l’aire molt ràpidament, però no a l’instant. El fenomen de l’eco va alimentar les primeres reflexions: si la propagació del so fos instantània no podríem distingir el so inicial del so reflectit en una paret.
Aristòtil ja va intentar donar una explicació del so igual que a molts altres fenomens de la física, però no es va sortir prou bé i els escolàstics van difondre les seves idees durant tota l’Edat Mitjana. Per exemple, Aristòtil creia que els sons de distints tons tenen velocitats diferents. No va ser fins 1624 que Gassendi, mesurant la velocitat del so, va mostrar que els aguts i els greus es propaguen amb la mateixa velocitat.
El primer mètode acceptable emprat per a determinar la velocitat del so utilitzava un canó. Un observador damunt un un tossal, mesurava el lapse transcorregut entre el moment en que veia la deflagració i escoltava el tret del canó. Coneixent la distància al canó, podia calcular la velocitat del so. Aquest procediment donava molts problemes ja que el vent lateral desviava l’ona sonora, que descrivia, per tant, una trajectòria corba, o frenava o augmentava la velocitat del so si anava en la mateixa direcció. A més, les variacions de temperatura pel camí originaven refraccions que apartaven l’ona sonora de trajectòria rectilínia.
I no acaben aquí les dificultats. El so pot refractar-se de la mateixa manera que la llum canviant de velocitat, i per tant de direcció, en passar d’un mitjà a un altre, fins i tot concentrar-se en un focus com en la lent de Sondhauss feta amb un globus ple d’anhídrid carbònic. Així, el so es propaga més ràpidament en l’aire calent que en l’aire fred, la qual cosa dóna lloc a les zones de silenci. Per exemple, s’explica que en 1923 el so de l’explosió d’una fàbrica de municions d’Holanda va ser oït a distàncies superiors a 800 km, però en canvi no va ser escoltat a la zona compresa entre els 100 160 km perquè l’ona sonora que es propagava al llarg del sòl es va debilitar aviat. El so escoltat a majors distàncies era el produït per l’ona sonora que s’havia propagat cap a les zones superiors de l’atmosfera i refractat cap avall en travessar la capa d’aire calent.
No obstant els valors que s’obtenien per a la velocitat del so eren majors que el que havia proposat Isaac Newton als seus Principia (Philosophiae Naturalis Principia Mathematica, 1686) i eren ficats en dubte donada l’autoritat del gran físic. Newton havia fet la primera determinació analítica de la velocitat del so a les proposicions 48, 49 i 50 del Llibre II dels Principia. Per a l’aire al nivell del mar a una temperatura ambient típica va calcular un valor de de 298 m/s, que és com un 15% més baix del valor real.
Per explicar aquesta diferència s’han d’introduir diverses propietats no ideals dels gasos, el que va fer Laplace al 1816 corregint-hi les deficiènciaes en l’anàlisi de Newton, com que el procés del moviment de so no és isotèrmic, sino adiabàtic. Malgrat tot, el mètode bàsic concebut per Newton era essencialment correcte. Un estudi al respecte el teniu a Laplace and the Speed of Sound, de Bernard S. Finn.
La determinació de la velocitat del so a l’aire lliure era important per molts motius, per exemple per raons militars ja que el seu coneixement permetia localitzar la distància a la que es trobava l’artilleria enemiga. Per això van ser continus els intents per calcular-la, encara que fins mitjans del segle XIX no es va fer uns càlculs suficientment bons amb els experiments realitzats per M. Regnault, tal i com explica Guillemin.
Regnault va utilitzar un equip amb un artifici elèctric per a la mesura del temps. L’experiment es va realitzar en una galeria subterrània, en les proximitats de París. El tret d’un fusell trencava el fil d’un circuit, creuat a la boca de l’arma, i llavors es movia un plomí tintat sobre un tambor registrador, situat a l’extrem del tub. Quan el so arribava allí, vibrava un diafragma, i aquest moviment també era registrat al tambor. Ja que la velocitat de rotació d’aquest era coneguda, es calculava fàcilment la del so.
Com hem vist en aquesta entrada, actualment els pot determinar en un laboratori escolar la velocitat del so a l’aire de moltes diverses maneres i amb resultats que fa segle i mig sortirien als diaris. Animeu-vos a utilitzar-les!
Mesura de la velocitat del so a l’aigua
La propagació del so a l’aigua va ser negada durant molt de temps perquè no es reconeixia la comprensibilitat i l’elasticitat dels líquids. Per primera vegada es va mesurar la velocitat el so a l’aigua al llac de Ginebra al 1827 pel físics Colladon i Sturm. Es colpejava una gran campana a sota de l’aigua alhora que es produïa la ignició d’una càrrega de pólvora. Un observador, usant un otòfon cobert con una membrana, l’extrem de la qual estava submergit a l’aigua, mesurava el lapse transcorregut entre el moment en què es veia la fogonada i el moment en què escoltava la campana. L’experiment es feia en una gran extensió d’aigua, perquè en ella la velocitat del so és relativament alta: al voltant de mil sis-cents metres per segon.


És important conèixer el valor exacte de la velocitat del so a l’aigua, per a dissenyar aparells de sondeig. Els mètodes actuals utilitzen explosions de càrregues simultànies a un senyal de ràdio. L’arribada del so es detecta mitjançant hidròfons (micròfons usats davall l’aigua) i es mesura l’interval transcorregut. Els sons no cessen a l’aigua tan ràpidament com en l’aire y aconsegueixen distàncies molt més grans. Per això, és possible sentir que el so de les hèlices d’un vaixell a una distància de 15 a 18 quilòmetres.