És coneixement tradicional que si la punta d’una vareta s’aparta de la seva posició d’equilibri i es deixa anar estant fix l’altre extrem, comença a vibrar i produeix un soroll, el que s’ha aprofitat per construir instruments musicals, per exemple els lamel·lòfons com la sansa.

Guillemin en El Mundo Físico es feia eco del fenomen fa 150 anys, com es veu al dibuix de sota, encara que llavors era una mica complicat estudiar quantitativa i experimentalment les vibracions de varetes. Malgrat aquestes dificultats, les deformacions i vibracions de bigues han estat objecte d’estudi teòric i pràctic continu per la seva importància en disseny d’estructures en els camps de la enginyeria i l’arquitectura.

Encara que no apareixen sovint als llibres de text de secundària, alguns d’aquests estudis estan relacionats amb noms de científics famosos. Així, Galileo Galilei (1564 – 1642) va estudiar la resistència dels sòlids al trencament a la jornada segona del seu llibre Consideracions i demostracions matemàtiques sobre dos noves ciències on discuteix el comportament de la biga en voladís sota el seu propi pes i una carrega concentrada a l’extrem. La llei de Hooke (1635 – 1703), una de les més importants lleis de la mecànica dels materials, planteja, com tots sabem, que l’allargament unitari que pateix un material elàstic és directament proporcional a la força que se li aplica. Jakob Bernoulli (1654 – 1705) va estudiant la forma de la corba d’una barra elàstica flexionada i va deduir la seva equació, i també va descobrir l’eix neutre, encara va ser Edme Mariotte (1620 – 1684) qui va desenvolupar el concepte. Charles August Coulomb (1736 – 1806) va publicar el primer anàlisi que avui es considera correcte dels esforços d’una biga amb secció rectangular. Thomas Young (1733 – 1829) va introduir per primera vegada el concepte de Mòdul d’Elasticitat i també va tractar problemes de torsió d’eixos i flexió de bigues en voladís. Etc., etc.

Pot ser podria ser interessant que l’alumnat de secundària tractés també algun aspecte de la flexió i vibració de barres, i més quan avui en dia tenim al nostre abast tota la parafernàlia de les noves tecnologies que ens poden ajudar a estudiar experimentalment algun dels factors dels que depèn la freqüència de vibració de les varetes (fleixos, barretes, llengüetes, etc.) agafades per un dels seus extrems, i és el que repasso a continuació.

• Mesura de la freqüència de vibració mitjançant un fotointerruptor
• Mesura de la freqüència de vibració mitjançant el so que produeix
• Mesura de la freqüència gracies a la vibració mecànica que produeix
  • Mesura de la massa d’un objecte fixat a l’extrem de la vareta
  • Mesura de la massa d’un objecte pel seu pes en penjar-lo de l’extrem de la vareta
• Mesura de la freqüència de vibració pel desplaçament de la vareta en la vibració
• Vibració forçada. Una altra possibilitat de conèixer la freqüència de vibració

Freqüència de vibració de les varetes

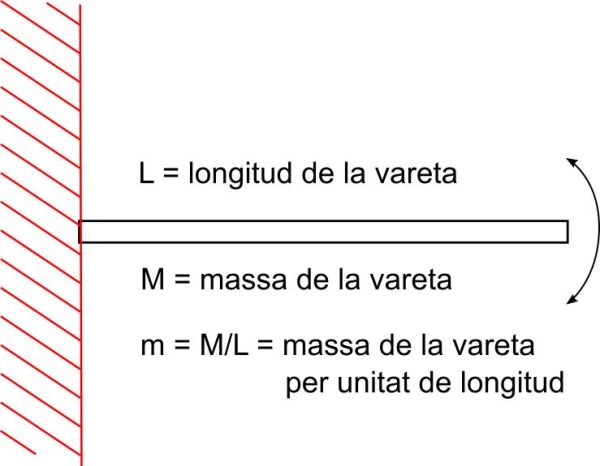
El professor argentí Salvador Gil ens ofereix al capítol 20 del seu llibre Experimentos de física de bajo costo usando las TICs l’estudi de la vibració de barres. La conclusió a la que arriba és que la freqüència de vibració d’una vareta agafada per un extrem depèn de la seva longitud i de la seva densitat lineal (massa dividida per la longitud) entre altres coses (també podeu acudir al Curso Interactivo de Física en Internet del professor Angel Franco).

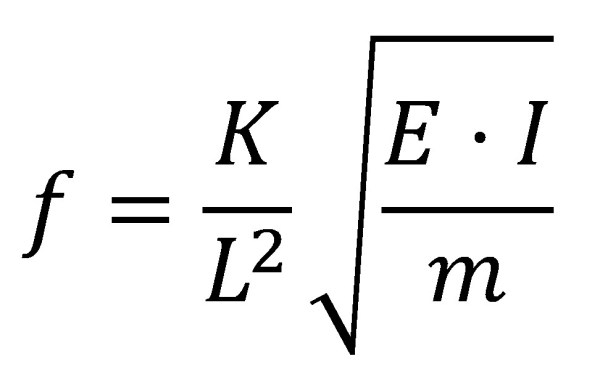
On f és la freqüència de vibració, E és el mòdul de Young, que depèn del tipus de material, I és el moment d’inèrcia de la sección trasversal respecte de la fibra neutra de la vareta, L és la longitud i m és la seva densitat lineal.

A l’equació es pot veure el sentit de la influencia de cadascun dels components del sistema en el valor de freqüència. Així, la freqüència augmentarà quan disminueix la longitud, augmenti la rigidesa del material o disminueix la massa. En concret, la freqüència ha de ser directament proporcional a la inversa de la longitud al quadrat.

Mesura de la freqüència de vibració mitjançant un fotointerruptor

En el mateix capítol 20, en el projecte 54, Salvador Gil proposa un disseny experimental per estudiar la relació entre la freqüència de vibració i la longitud de barres que vibren amb un extrem lliure, disseny amb dues variants per a mesurar la freqüència: una utilitzar un fotointerruptor col·locat a prop de l’extrem lliure de la barra, i una altra consistent en pegar a la vareta un imant a prop del seu extrem fix i mesurar el seu moviment amb un sensor Hall.

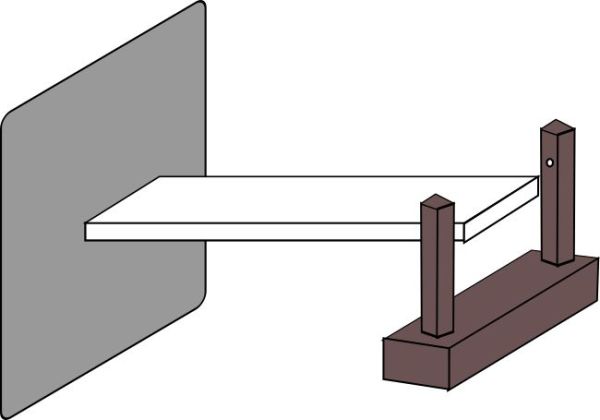
Els alumnes Pablo Adrián Nuñez, Gabriela Lohr i Tamara Werhun, 2005, exemplifiquen en el treball Determinación del módulo de Young el cas del fotointerruptor, obtenent valors dels mòduls de Young per a diferents materials una mica allunyats dels establerts per la comunitat científica i analitzen les possibles causes.

Causes que al parer de Sanchez, M. A. i altres en La flexibilidad de empotramientos “rígidos” y su influencia en la determinación de la primera frecuencia natural de una viga (2012) poden tenir a veure amb la diferència entre les condicions de contorn teòriques per a l’obtenció de les equacions i les condicions de contorn reals dels experiments que fan (i que farem nosaltres), per exemple la fermesa de la subjecció de les varetes per un dels seus extrems.

De totes maneres, una cosa és el càlcul d’un valor concret, com és el mòdul de Young, i una altra és la relació entre variables que sí que s’ajusta prou bé als models.

Mesura de la freqüència de vibració mitjançant el so que produeix

Si es fa vibrar un fleix agafat a la mà gaire bé no se sent res i s’extingeix la vibració ràpidament, però si la vareta o el fleix es lliga a una taula, per exemple prement-los amb els dits, la taula actua com a una caixa de ressonància i es sent molt bé el so que produeix la vibració.

Per a mesurar les freqüències es pot utilitzar un telèfon i qualsevol aplicació que sigui capaç d’analitzar els sons i indicar mitjançant un anàlisi de Fourier els valors de les freqüències que els constitueixen. A mi m’agrada particularment Advanced Spectrum Analyzer Pro perquè permet amb l’opció Enable Peak Hold mantenir en pantalla l’espectre del so una vegada ha deixat de sonar i analitzar-lo tranquil·lament.

Una alternativa és gravar el so en un ordinador i analitzar-lo amb el programa Audacity, però és un procediment molt més feixuc que quan s’utilitza el telèfon o la tauleta. Malgrat això, és el que fan Pérez, N. I altres en Determinación de la frecuencia natural de vibración de una barra. Parte 1, estudio experimental utilizando tarjeta de sonido. Per aconseguir una millor gravació dels sons lliguen la vareta a una mordassa i la col·loquen sobre la pantalla de l’ordinador portàtil ja que és allí on es troba el micròfon.

Tenint en consideració les limitacions dels micròfons dels dispositius mòbils, la freqüència mínima que ha de tenir la vibració per poder ser mesurada ha de ser de 20 Hz, preferiblement més, així que per longituds llargues de les varetes que les fan vibrar més lentament s’hauran d’utilitzar altres opcions, com pot ser gravacions en vídeo, fotoportes, com ja he comentat, o mesura del canvi de posició de l’extrem, que veurem més endavant, per exemple.

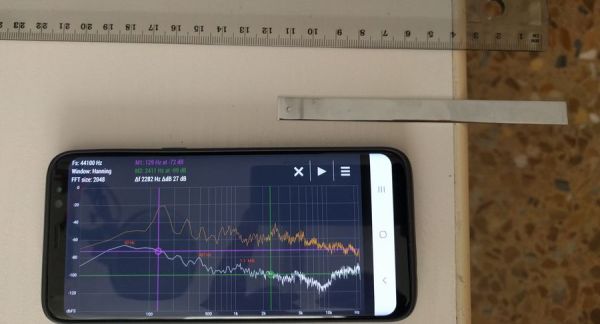
En el cas del fleix de la foto de dalt he obtingut els següents valors de freqüència per a diferents longituds de vibració:

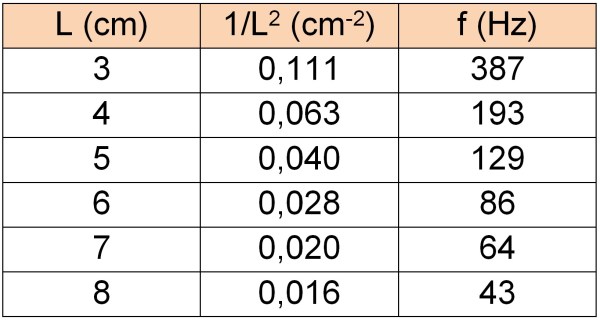
Que si es grafiquen mostren una bona correlació entre la longitud de la vareta que vibra i la freqüència a la que ho fa.

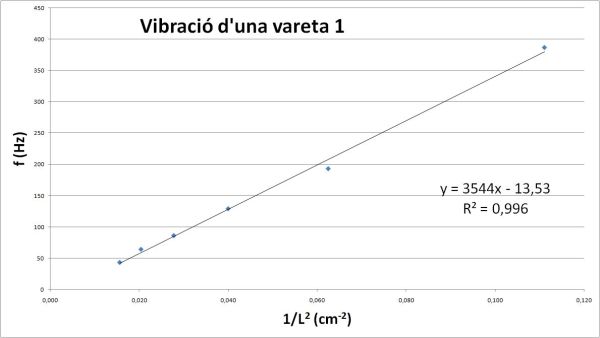
Mesura de la freqüència gracies a la vibració mecànica que produeix

En un dels experiments descrits a l’article de Sanchez, M. A. i altres que he citat a dalt, utilitzen per a mesurar la freqüència de vibració un sensor acceleròmetre connectat a un ordinador. És una possibilitat que Julien Bobroff reorienta proposant que s’utilitzi com acceleròmetre el que porten els telèfons mòbils.

En el vídeo, Frédéric Bouquet, col·lega de Julien Bobroff, mesura la freqüència de vibració d’un regle metàl·lic amb l’aplicació Phyphox, que incorpora la possibilitat de mesurar la freqüència amb la que vibra el telèfon. La eina Espectro de aceleración permet veure en temps real a la pestanya Espectro la freqüència fonamental de la vibració del mòbil gràcies a una transformada de Fourier, i a la pestanya Historia les freqüències fonamentals al llarg del temps.

Per a que el telèfon noti la vibració de la vareta s’ha de ficar recolzant-se al fleix tal i com mostra la fotografia de sota. A la pestanya Espectro es veuen els pics de la vibració i va bé per fer-se una idea del valor de la freqüència a la que vibra el fleix per a cada longitud que sobresurt de la taula, però per a trobar el valor concret s’ha de anar a la pestanya Historia ja que allí es mantenen els punts quan s’atura la mesura.

Amb el fleix de la foto he obtingut valors com els de la taula de sota, que portats a un full de càlcul donen una gràfica en la que es veu que la freqüència de vibració de la vareta és inversament proporcional a la seva longitud al quadrat, el que coincideix amb els pressupostos teòrics.

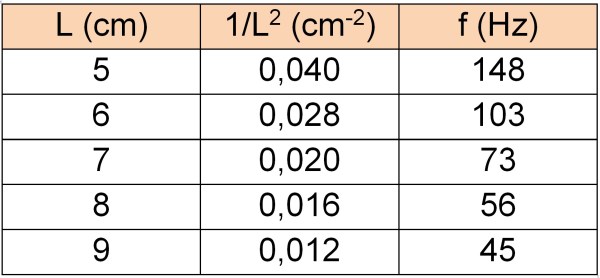
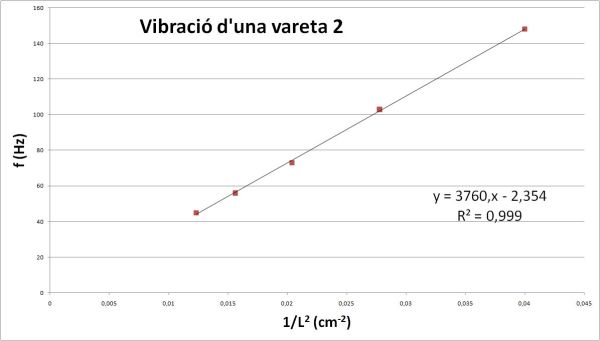
Mesura de la massa d’un objecte fixat a l’extrem de la vareta

En la conversa dels professors Julien Bobroff i Frédéric Bouquet en el vídeo de dalt, plantegen la possibilitat de mesurar la massa d’un objecte enganxant-lo a la punta d’un fleix i fent-lo vibrar.

La freqüència de vibració d’una vareta amb una massa enganxada a l’extrem lliure, menyspreant la massa de la vareta, ve donada per:

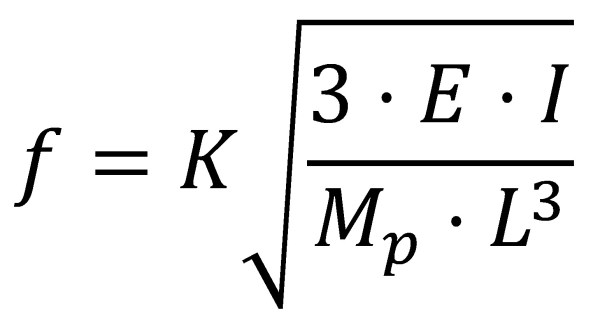
I sense menysprear la massa de la vareta, la freqüència serà:

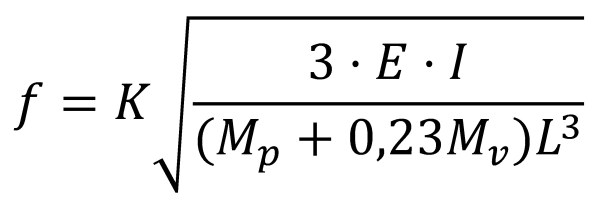
On f és la freqüència de vibració, L és la longitud del fleix, M_p és la massa enganada a la punta i M_v és la massa de la vareta. Tant en una equació com a l’altra es pot veure que la freqüència augmentarà quan disminueix la massa, en concret que la freqüència és directament proporcional a l’invers de l’arrel quadrada de la massa.

Quant a la consideració o no de la massa de la vareta en els càlculs, resulta imprescindible si es vol mesurar la massa d’un objecte comparant com vibra la vareta amb i sense, però los resultats en aquest cas no s’ajusten prou bé a l’esperat. Per una longitud de fleix de 7 cm (3,8 g) i amb dues masses, una goma de 6,6 g i un caramel de 3,7 g, he obtingut les freqüències de 73 Hz (la vareta sola), 29,5 Hz (amb la goma) i 39 Hz (amb el caramel). En substituir a l’equació i fer els càlculs s’obtenen unes masses de 5,4 g per a la goma i 3,1 g per al caramel, que són de l’ordre però una mica allunyades.

Una altra cosa és si es compara la massa d’un objecte amb la d’un altre. Aquí es pot menysprear la massa de la vareta i considerar només les masses enganxades a l’extrem, de manera que per una mateixa vareta i una mateixa longitud, el producte de la freqüència a la que vibra per l’arrel quadrada de massa enganxada sempre dóna aproximadament el mateix valor:

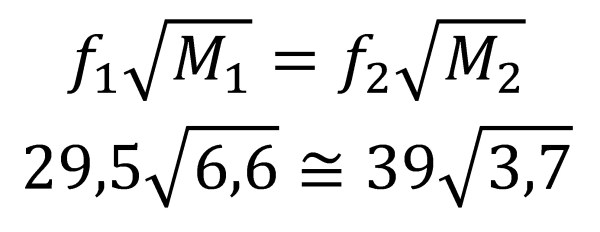
Mesura de la massa d’un objecte pel seu pes en penjar-lo de l’extrem de la vareta

S’ha pogut observar en diferents treballs citats més amunt que molts d’ells acompanyen els estudis de vibració de varetes encastades horitzontalment amb els corresponents a la seva flexió estàtica com a conseqüència de penjar pesos a l’extrem lliure, per exemple la proposta de Gil al projecte 51 del capítol 20.

Pot ser és més fàcil/intuïtiu per l’alumnat de secundària mesurar el pes dels cossos per aquest sistema que no amb la vibració, de forma similar a que és més fàcil/intuïtiu obtenir la massa d’un objecte penjant-lo d’un dinamòmetre com ho fem en estudiar la llei de Hooke, que estudiant el moviment oscil·latori amunt i avall de l’objecte penjat d’una molla.

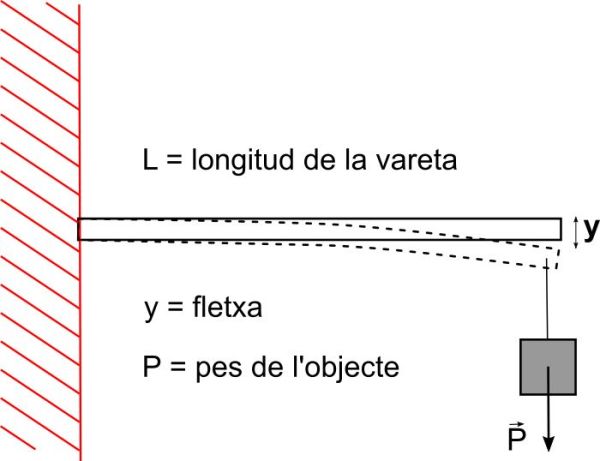
Per a petites deformacions que no arribin a deformar permanentment la vareta es té que la força realitzada a l’extrem pel pes que es penja, és directament proporcional a la deformació que produeix, és a dir al desplaçament en vertical de la punta de la vareta (Gil, 2016; Franco, 2015; Beléndez i al., 2002).

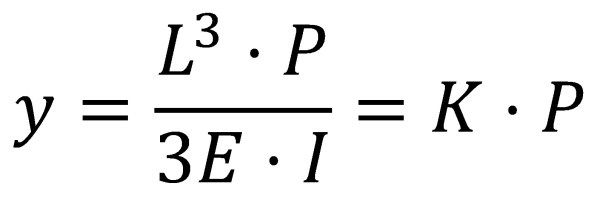
On y és el desplaçament vertical a l’extrem de la vareta (la fletxa), L la longitud de la vareta, E el mòdul de Young, I el moment d’inèrcia de la secció transversal respecte de la fibra neutra i P el pes aplicat a la punta. Per una determinada vareta L, E i I tenen un valor determinat, amb la qual cosa es poden englobar en un valor constant.

El magnífic llibre Experimentos con hilos y cinta adhesiva, d’Edge, R.D. (2002) descriu a l’Experimento 1.05 – Fuerzas elásticas un protocol per a trobar el valor de la constant elàstica, K, amb una regla.

Aquesta forma de trobar la massa només servirà en situacions en les que actuï la gravetat i no en cassos d’ingravidesa, com fora el pesar els astronautes a l’espai exterior. Fa temps (2008) l’ESA va llançar el programa Lleve su aula al espacio i entre les seves activitats va elaborar i distribuir un kit amb el mateix nom, que contenia una balança per mesurar masses consistent en dues molles que s’agafaven a l’objecte per dos costats oposats i, en fer-les oscil·lar, la freqüència d’oscil·lació servia per a mesurar la massa del cos. Un sistema amb una barra que vibrés també serviria.

La NASA, però, no utilitza cap dels dos sistemes. Des de 2005 fa servir el Dispositiu Espacial per a Mesurar Masses per Acceleració Lineal (SLAMMD, Space Linear Acceleration Mass Measurement Device) que consisteix en dues molles fortes que empenten l’astronauta mentre uns sensors òptics mesuren l’acceleració que pateix. Segons @Wicho l’acrònim slammd sona una mica com slam (cop) i per això, pot ser, l’han anomenat així.

Mesura de la freqüència pel desplaçament de la vareta en la vibració

Una altra manera d’obtenir la freqüència de la vibració quan els desplaçaments de l’extrem de la vareta són prou grans per mesurar-los amb un sensor de distància és utilitzar un sensor d’aquest tipus connectat a Arduino fent la funció de telèmetre. Ja he explicat en Connectar Arduino i Phyphox: Termòmetre i telèmetre com fer per instal·lar el codi i aconseguir els valors de distància en la pantalla del telèfon mòbil.

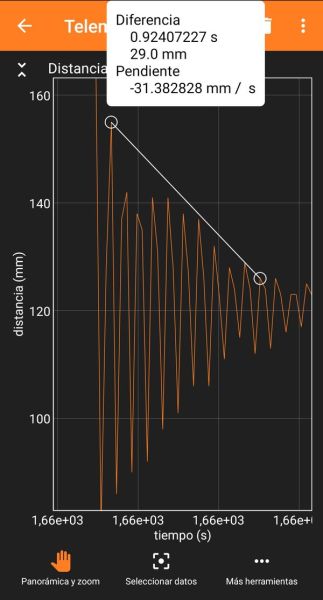
Si es realitza un muntatge com el de la fotografia de dalt, es desplaça el fleix de la seva posició d’equilibri i després es deixa anar, vibrarà i es podran obtenir per a cada longitud unes dades com les de la captura de pantalla del costat. He obtingut aquests valors amb un fleix de 17,5 cm de longitud. Es veu que el temps transcorregut en 10 oscil·lacions és de 0,924 s, el que dóna una freqüència de 10,8 Hz.

Quan mesurava la freqüència amb el so que produeix la vibració he obtingut per aquets mateix fleix un valor de 129 Hz per a una longitud de vareta de 5 cm. Si el producte de freqüència per longitud al quadrat s’ha de mantenir constant, s’obté:

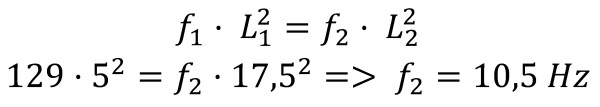
Valor que indica que els mètodes són equiparables. Aquest per a freqüències baixes i desviacions grans de d’extrem de la vareta, i el del so per a freqüències altes.

Vibració forçada. Una altra possibilitat de conèixer la freqüència de vibració

Una possibilitat alternativa a les que hem vist fins ara és la de fer vibrar la vareta forçadament i observar per a quines freqüències entra en ressonància i les amplituds de vibració és fan més grans.

És el que proposen C.E. Repetto, A. Roatta i R.J. Welti en Medición de frecuencias de resonancia, factor de pérdida y módulo de Young dinámico de varillas empotradas, on es forcen les vibracions amb un vibrador de la casa Pasco que incorpora una sèrie de fleixos de diferents longituds.

D’una manera més limitada, ja que només es disposa de la freqüència de 50 Hz del corrent altern de la xarxa elèctrica, ja ho feia el manual d’Ondas Mecánicas y Vibraciones d’Enosa (1968), on el protocol 7.2 Vibraciones de varillas – Frecuencímetro proposa forçar la vibració amb una bobina amb nucli de ferro connectada al corrent i col·locada a prop del fleix, que en aquest cas està en posició vertical, tal i com il·lustra el dibuix.

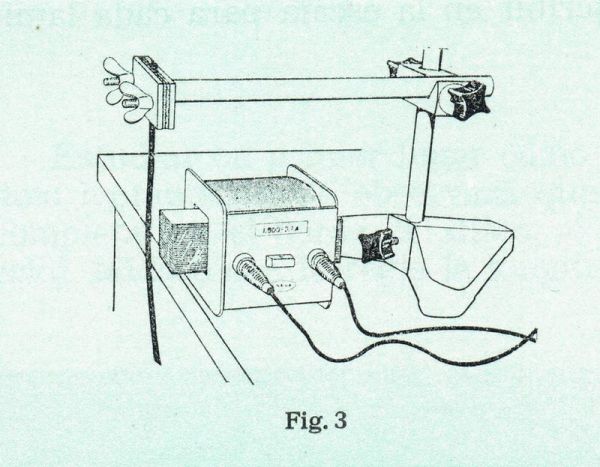
El freqüencímetre o galvanòmetre de vibració del que parla aquest últim protocol és un instrument que en la seva versió clàssica encara s’utilitza per a controlar el voltatge de les xarxes elèctriques. Si el voltatge que s’ha de subministrar és a 50 Hz, el freqüencímetre indica valors de tensió al voltant del valor nominal que interessi, de 50 més/menys 3 Hz en el cas de l’aparell de la fotografia.

L’esquema del seu funcionament es representa en el dibuix de sota on s’han col·locat diversos fleixos de material ferromagnètic de longituds diferents, però que no difereixen massa. Longituds que estan calculades per entrar en ressonància amb el doble de la freqüència del corrent que passi per la bobina, ja que l’electroimant atrau el material ferromagnètic tant si el corrent (que és altern) va en un sentit com en un altre, és a dir tant si es genera un pol nord com si és un pol sud.

---

---