Els passats dies 31 d’octubre i 1 i 2 de novembre va tenir lloc a Màlaga la XIX Reunión de Divulgadores (DDD) que, com cada any va estar fenomenal, i això que vaig participar jo amb una ponència 😉 .

Com sabeu els que me seguiu, l’encontre consisteix en diverses activitats, però les centrals son dues sessions en les que els ponents han d’exposar la seva contribució en un màxim de cinc minuts. Aquest any la meva la vaig titular Dos experiments: un clàssic i un altre quàntic, i la teniu aquí sota. La resta d’actuacions les teniu en el canal DDD de YouTube i el resum de les comunicacions aquí.

El vídeo comença amb una referència a l’existència d’un asteroide que te el nom de Cosialls en honor al nostre company Anicet Cosialls. La història de com ha arribat a succeir això és molt bonica: que un alumne et reconegui la feina com a professor anys després d’haver-te tingut és molt gratificant. El diari Segre de Lleida va fer un ampli reportatge al respecte en el que s’explica com ha estat possible que un lleidatà viatgi per l’espai en companya d’altres científics cèlebres, com Einstein o Laplace.

Dels dos experiments del títol de la miniponència, el quàntic és el dels tres polaritzadors que ja vaig explicar en una entrada anterior d’aquest bloc: Llum polaritzada i física quàntica. L’experiment clàssic és el de dues boletes en un pla inclinat, que és al que es refereix el títol d’aquesta entrada, i és en el que me detindré una mica a continuació.

Caiguda de boles per un pla inclinat

Si deixem una bola sobre un pla inclinat comença a rodar cap a baix cada vegada a més velocitat. És el que s’observa en el vídeo de sota en els dos primers casos.

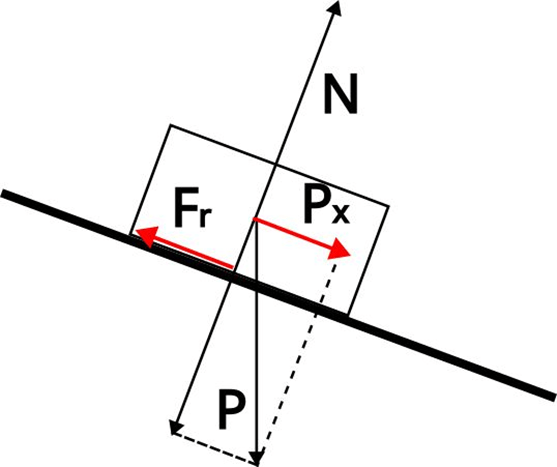
Aquest moviment ens sembla lo més natural, però si en lloc d’una boleta fora un tac prismàtic de goma no rodaria, en tot cas lliscaria o es quedaria quiet depenent de que la força de fregament fora més petita o igual a la component del pes del tac en la direcció paral·lela al pla.

Però la bola sempre roda, primer perquè és una bola (que diria un alumne avantatjat 😉), i per que aquí la força de fregament contribueix al moment de les forces que fa girar la pilota:

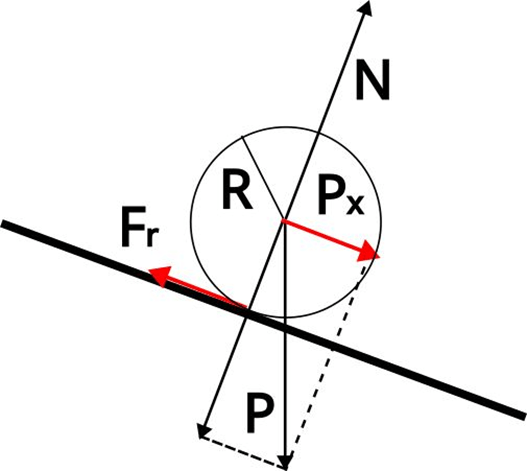
Fr·R = I·α, si agafem com a centre de gir el centre de la boleta

on I és el moment d’inèrcia de l’esfera (I= 2·m·R²/5) i α és l’acceleració angular a la que es veu sotmesa la bola, com ens explica Angel Franco.

La mateixa lògica podem aplicar al cas tercer en el que deixem anar dues boletes pel pla inclinat de manera que les dues roden cap a baix. Però què passa en la quarta situació del vídeo en la que en deixar les dues boles es queden parades?

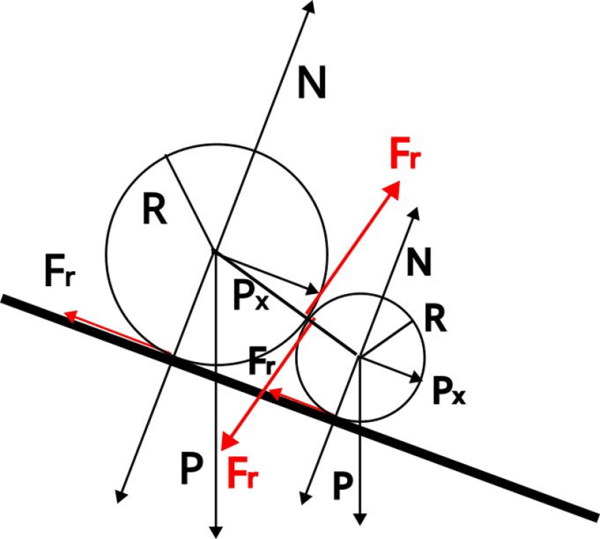
La clau està en que ara la força que exerceix la bola gran sobre la petita és prou gran per aconseguir una força de fregament màxima entre les boles més gran que la força de fregament de cada esfera amb el pla inclinat, de manera que el moment total de les forces sobre cada bola és zero.

En el cas de que la bola petita estigui damunt la gran, la pressió entre les boles és prou petita com per a que la força de fregament per lliscament entre les boletes sigui més petita que la força de fregament amb el terra. En aquest cas el moment no és zero i comencen a rodar.

---