Experiments a l’Any Internacional de la Ciència i la Tecnologia Quàntica 2025 (IYQ2025).
- Difracció per dues escletxes
- Difracció per una escletxa simple
- Difracció de la llum per una escletxa i principi d’incertesa de Heisenberg
En aquesta entrada començaré parlant de dos dels experiments més emblemàtics que han marcat fites en la nostra comprensió de la Física. I no només són importants en la història de la ciència sinó que son molt xulos, tant és així que van ser considerats dos dels experimentes més bonics de la Física (el més bonic de tots i el cinquè) a l’enquesta que va fer Robert P. Crease al 2002.
L’experiment de doble escletxa de Thomas Young, realitzat el 1801, que va demostrar de manera contundent el caràcter ondulatori de la llum. Amb un muntatge senzill Young va fer passar un feix de llum per banda i banda d’una carolina estreta i va observar en una pantalla el característic patró de franges alternades, conseqüència de la interferència. Aquest experiment va servir per desafiar la visió corpuscular newtoniana de la llum, impulsant l’acceptació del model ondulatori.
El 1927, l’experiment de Davisson i Germer va replicar de manera indirecta aquest tipus de comportament ondulatori dels fotons per al cas dels electrons. En fer incidir un feix d’electrons sobre un cristall de níquel, van observar un patró de difracció que evidenciava que els electrons mostraven propietats ondulatòries, fet que recolzava la proposta de De Broglie, pedra angular de la mecànica quàntica.
No va ser fins la dècada dels 60 que es va realitzar una versió tal qual de l’experiment de doble escletxa emprant electrons, cosa que va permetre observar directament un patró d’interferència característic dels fotons, encara que els electrons s’arribessin a disparar d’un en un. L’experiment va ser dut a terme pel físic alemany Claus Jönsson i es va realitzar a l’Institut de Física de la Universitat de Tübingen, a Alemanya, al voltant de 1961. Aquest experiment, encara que a aquelles alçades del desenvolupament de la mecànica quàntica no va ser crucial, és magnífic per analitzar els fonaments de la mecànica quàntica i comprendre la naturalesa probabilística i dual de la matèria.
Jo no us proposo de treballar amb electrons sinó d’utilitzar fotons i fer-los passar per una doble escletxa, unificant els dos experiments.
També parlarem de la difracció de la llum per una única escletxa i com podem fer servit aquest experiment per a comprovar el principi d’indeterminació de Heisenberg. I, ja posats, veurem que passa si anem augmentant el número d’escletxes per les que fem passar la llum, per exemple si utilitzem una xarxa de difracció.
El principi d’indeterminació de Heisenberg estableix que certs parells de variables físiques conjugades, com ara la posició (x) i el moment lineal (p) (o l’energia i el temps), tenen una incertesa mínima en mesurar-les alhora que s’expressa formalment per la desigualtat
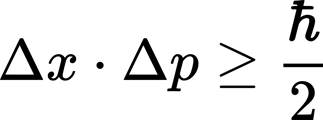
on Δx i Δp són les incerteses en la posició i el moment, respectivament, i ħ és la constant reduïda de Planck (h/2π). Això significa que com més exactitud intentem assolir en la determinació de la posició d’una partícula, més gran serà la incertesa en el seu moment, i viceversa. L’arrel d’aquesta limitació no és una deficiència dels nostres instruments de mesura sinó una conseqüència inherent a la naturalesa ondulatòria de les partícules i de la descripció probabilística de la realitat quàntica.
Aquest principi no diu que les partícules no tinguin una posició o un moment definits en algun sentit ontològic, sinó que la teoria quàntica només ens permet predir la probabilitat d’obtenir certs valors en fer un mesurament. Però no es tracta simplement d’un efecte de la pertorbació causada en mesurar, encara que en experiments concrets, per exemple, en utilitzar fotons per localitzar un electró, la interacció altera el sistema, sinó d’una limitació fonamental sorgida del fet que les magnituds en qüestió corresponen a operadors quàntics que no commuten. Això vol dir que la impossibilitat de conèixer tots dos valors amb precisió arbitrària és una característica intrínseca de la descripció matemàtica dels sistemes quàntics, i no merament un “error experimental” que pogués eventualment superar-se amb millors aparells.
Difracció per dues escletxes
Experiment de la interferència de la llum fet per Young
Començarem per l’experiment més facilet de fer ja que amb un bocinet de cartolina negra tenim prou. Com he dit, Young no va utilitzar dues escletxes en una làmina per les quals passar la llum, més aviat el que va fer és aconseguir amb un forat un feix de llum el més fi i lluminós possible i encaminar-lo a un tarja fina (de 0,85 mm de gruix) de manera que la tarja el tallava i part del feix la recorria per un cantó i l’altre part pel cantó oposat. Quan els dos feixos resultants es tornaven a ajuntar produïen en una pantalla un patró d’interferència de franges clares i fosques, acolorides les de les bandes. Això és possible ja que el feix de llum blanca (amb tots els colors de l’arc de Sant Martí) aconsegueix coherència al fer-se primet i amb prou distància des de la font de llum (forat).
La proposta que us faig és encara més senzilla ja que no requereix aconseguir un feix de llum adequat. Només agafar una tita de cartolina negra prima d’uns 5×2 cm i ficar-la de cantó davant un ull (amb l’altre tancat) de cara a una paret clara. A tots dos costats de la cartolina veureu una sèrie de bandes clares i fosques produïdes per la interferència de la llum després de passar per les dues cares de la cartolina.
Alternativament, feu passar la llum d’un làser per una cartolina de cantonada i veureu una figura de difracció en una pantalla.

Igual que en passar per una cartolina prima, la llum es difracta en passar per un fill prim. El patró de difracció que surt és igual que el que sortiria en passar la llum per una escletxa (del que parlaré més endavant) de la mateixa amplada que el gruix del fil, com es pot demostrar matemàticament (principi de Babinet). Aquí teniu un vídeo en el que la llum és difractada per un cabell, que és un cas similar a l’original de Young (mireu també l’article de 2023 de Monteiro).
Interferència de la llum per dues escletxes
Per a realitzar l’experiment de la interferència de la llum en passar per dues escletxes necessitem una llum, una barrera amb dues escletxes i una pantalla per a recollir l’espectre que es forma:

Una font de llum ha de ser d’un làser ja que és monocromàtica, és a dir, d’un sol color, una sola longitud d’ona, λ, i no llum blanca (com va fer Young) que en estar formada per un continu de freqüències no produeix un espectre nítid. A més, la llum làser és coherent, el que vol dir que les ones de llum mantenen una relació de fase constant entre si el que facilita les interferències nítides.
Un punter làser vermell de poca potència és suficient (<5 mW). Es pot comprar a les botigues de tot a 100 i per internet a baix cost (millor si van amb piles AAA) i a la caixa normalment indiquen la longitud d’ona a la que emeten la llum. Per encendre’ls tenen un botó que es pot subjectar amb una agulla de roba, com en la fotografia.
La llum incideix sobre una barrera opaca que té dues ranures paral·leles, molt estretes i molt properes entre si de la que parlarem després. La separació entre els centres de les escletxes l’anomenarem d.
A una distància L de la barrera molt més gran que d es col·loca una pantalla blanca on s’observarà el resultat. És fàcil que L sigui molt més gran que d ja que d ha de ser petit. En tot cas, una distància L gran facilita els càlculs simplificant-los i fa que l’espectre sigui més gran amb el que és més fàcil realitzar mesures de distàncies entres màxims i/o mínims de llum a l’espectre i minimitzar l’error.
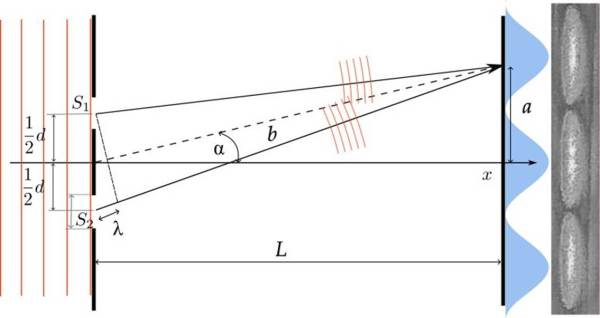
https://commons.wikimedia.org/wiki/File:Double-Slit_Experiment_%E2%80%93_sketch_of_geometry_and_definition_of_variables.svg
Si la llum fossin partícules esperaríem veure simplement dues línies brillants a la pantalla, directament darrere de cada escletxa, però a la pantalla no apareixen dues línies, sinó un patró de franges brillants i fosques alternades. A la franja brillant central li segueixen a banda i banda franges fosques, després d’altres brillants, després fosques, i així successivament.
Segons el principi de Huygens, quan l’ona de llum arriba a les dues escletxes, cada ranura actua com una nova font d’ones secundàries coherents. Aquestes dues noves ones es propaguen des de les ranures cap a la pantalla. A la pantalla, les ones provinents de les dues escletxes se superposen. Aquest fenomen de superposició es diu interferència.
Als punts de la pantalla on les crestes d’una ona coincideixen amb les crestes de l’altra les ones es reforcen tenint lloc una interferència constructiva, el que produeix una franja brillant (màxima intensitat). La diferència de camins recorreguts per les ones des de cada escletxa fins a aquest punt ha de ser un múltiple sencer de la longitud d’ona (Δr = m·λ, amb m = 0, 1, 2,…)
En els punts on les crestes d’una ona coincideixen amb les valls de l’altra, les ones es cancel·len mútuament produint-se una interferència destructiva, el que dona una franja fosca (mínima intensitat). La diferència de camins és un múltiple semi enter de la longitud d’ona (Δr = (m+1/2 )λ, amb m = 0, 1, 2,…)
Per trobar la posició de les franges brillants i fosques a la pantalla, necessitem conèixer la diferència de camins recorreguts pels raigs de llum des de cada escletxa fins a un punt a la pantalla. Si considerem el punt a la pantalla a una distància a del centre on es produeix el primer màxim de llum tindrem que serà α l’angle que sustenta a. Si la distància a la pantalla L és molt més gran que la separació entre franges a (L >> a), l’angle α serà molt petit i en aquest cas el sinus i la tangent són pràcticament iguals. Així (mireu el dibuix Difracció per dues escletxes):
sin α = tg α = a/L = Δr/d = λ/d
λ = d·tg α = d·a/L
Per a màxims successius la diferència de camins (Δr) ha de ser un múltiple de la longitud d’ona i per tant, en general:
m·λ = d·tg α = d·a/L, on m = 1, 2, 3 , …
Per als mínims (franges fosques): tenim que la diferència de camins ha de ser Δr = (2m+1)λ/2. Per tant d·sin α = (2m+1)λ/2 on m = 0, 1, 2,…i m=0 correspon a les primeres franges fosques a totes dues bandes del centre.

Podeu comprovar fins a quin punt les dades experimentals quadren amb l’equació deduïda a partir des valors corresponents als patrons de difracció que he obtingut amb dues dobles escletxes de 80 i 200 µm de separació respectivament (veure fotografies anteriors).

Si disposeu de làsers de llum de diferents colors (vermell, verd, blau) podreu comprovar com la separació entre màxims en la difracció varia de forma que va disminuint conforme la longitud d’ona del làser va disminuint del vermell al blau.
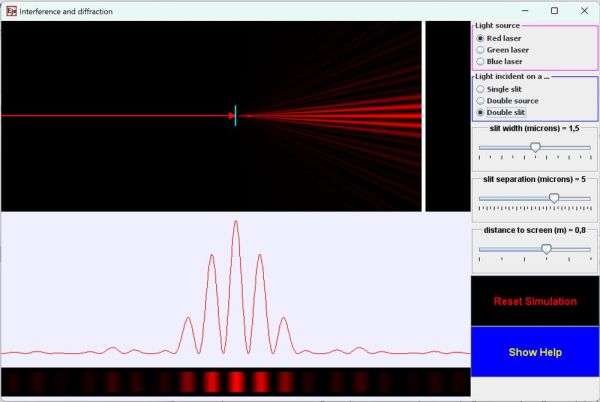
Alternativament a l’experimentació real teniu un parell de simulacions (entre altres que podeu trobar a internet) que m’agraden molt per estudiar quantitativament la difracció de la llum d’un làser a través de dues escletxes (i també d’una i de varies) a la web Compadre de l’Asociació americana de professors de física. Una és Diffraction and Interference Model: Single and Double Slits escrita per Andrew Duffy i l’altra Multiple Slit Diffraction Model, escrita per Fu-Kwun Hwang.
S’han de descarregar les aplicacions a l’ordinador (estan en format .jar) i per la seva execució s’ha de tenir instal·lat el programari Java de la casa Oracle.
Obtenció de dobles escletxes

1.- Una primera opció per a aconseguir una doble escletxa és fer-la en un quadradet de paper d’alumini amb un cúter. És fàcil, encara que s’ha de fer amb delicadesa. Es poden aconseguir dobles escletxes amb diferents distàncies entre elles però no molt juntes ja que es trenca la làmina entre les escletxes. En tot cas la distància entre les escletxes ha de ser prou petita per a que el feix de la llum del làser passi per totes dues alhora.
2.- Dobles escletxes de diversa mida i de distància controlada es poden obtenir també dibuixant-les amb un programa de dibuix com Inkscape i imprimint-les en blanc i negre en un acetat transparent adequat al tipus d’impressora o fotocopiadora que s’utilitzi. Les escletxes del dibuix de la vora les podeu baixar en aquest PDF i imprimir-les en qualitat alta (per tal que el negre sigui negre) al 100% d’escala (grandària real).
3.- També podeu comprar les escletxes a una casa de material educatiu de laboratori o per Amazon o Aliexpress. Tenen un preu assequible.
Difracció d’electrons en una doble escletxa
Nosaltres no podem fer l’experiment de la doble escletxa amb electrons perquè no tenim prous diners per comprar el material a una casa comercial (només el tub por costar més de 1000 €), però a la universitat els tenen i una d’elles, concretament el Departamento de Física Teórica de la de Valencia ens explica com ho fa i ens ofereix la possibilitat d’experimentar quantitativament amb una simulació i de veure el fenomen en vídeo.
No és ben bé l’experiment de la difracció per dues escletxes sinó la difracció dels electrons en un cristall de grafit policristal·lí, al estil del primer experiment de difracció fet per Davisson i Germer.
Per complementar l’experiment real teniu a continuació una animació que l’explica de forma deliciosa:
Difracció per xarxa
Si en lloc de tenir dues escletxes en una diapositiva en tenim vàries o moltes el fenomen que observarem serà el mateix que amb dues, però amplificat.
Si et situes a uns 50 cm d’una paret i, apuntant a la paret, fas passar la llum d’un punter làser a través d’un plàstic transparent s’observa únicament un punt corresponent al feix de llum del punter que travessa el plàstic. Però, si a continuació repeteixes l’experiència amb una xarxa de difracció que està formada per múltiples escletxes per mil·límetre veuràs un patró de difracció amb els màxims de llum molt més separats que en una doble escletxa donat que entre les línies de la xarxa la distància és menor que la distància entre les escletxes de l’experiment de la doble escletxa que hem fet anteriorment.

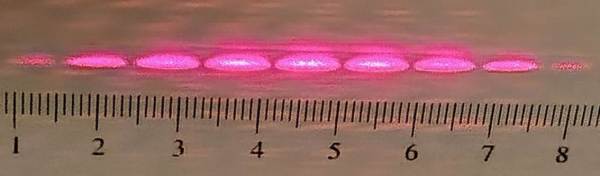
A la composició de sota s’aprecia com els màxims de llum es van fent cada vegada més concentrats conforme augmenta el número de ranures. Si a més es disminueix la distància entre escletxes els punt de llum es van separant cada vegada més, com es veu en la fotografia de dalt en la que la xarxa de difracció és un CD (de 625 línies per mil·límetre).
L’equació, però, que permet relacionar la distància entre línies en la xarxa amb el patró de difracció és la mateixa que hem deduït per la doble reixeta:
m·λ = d·a/L
on m = 1, 2, 3 , …, λ és la longitud d’ona de la llum del làser que utilitzem, a és la distància del màxim de llum central al punt de llum corresponent a m, L és la distància de la xarxa a la pantalla en la que es recull el patró de difracció i d és la distància entre les escletxes (línies) de la xarxa de difracció, que es calcula com l’invers del número de línies per mil·límetre (d = 1000/625 = 1,6 µm en el cas d’un CD).

Xarxes de difracció entre 100 i 1000 línies per mil·límetre es poden comprar en les cases comercials de de material de laboratori i per Amazon o Aliexpress per un preu raonable, però també es poden obtenir molt fàcilment a partir de CDs (≈ 625 línies/mm) o DVDs (≈ 1300 línies/mm), com explico en Construcció de xarxes de difracció a partir de CDs i DVDs.
Difracció per una escletxa simple
A l’experiment de la doble escletxa la llum que passa per una escletxa interfereix amb la llum que passa per l’altra. Però quan només hi ha una ranura en l’escletxa simple, amb què interfereix la llum que la travessa?
Senzillament, interfereix amb si mateixa. Si comparem la mida de l’escletxa amb la longitud d’ona del feix de làser, comprovarem que l’escletxa és unes 100 vegades més ampla. Per tant, té sentit que la llum d’un punt de l’escletxa interfereixi amb la llum de qualsevol altre punt. Però com és el patró de difracció en el cas de l’escletxa simple?
Amb una escletxa simple és més fàcil explicar primer els punts foscos, és a dir, els mínims del patró de difracció. Al dibuix de sota, la llum de la vora inferior de l’escletxa es troba tan sols una longitud d’ona per davant de la llum de la vora superior. Si dividim el feix de llum en dues parts, tindrem que a cada punt de la part superior del feix li correspon un punt a la part inferior, i que el desfasament de la llum entre la part superior i la inferior és de només mitja longitud d’ona. Per tant, tota la llum de la part superior interferirà de manera destructiva amb la llum de la part inferior. En aquesta direcció es poden apreciar els primers mínims del patró de difracció. Si la llum de la vora inferior de l’escletxa està 2, 3 o més longituds d’ona per davant de la llum de la vora superior passa el mateix, en aquests casos no s’apreciarà llum a la pantalla.
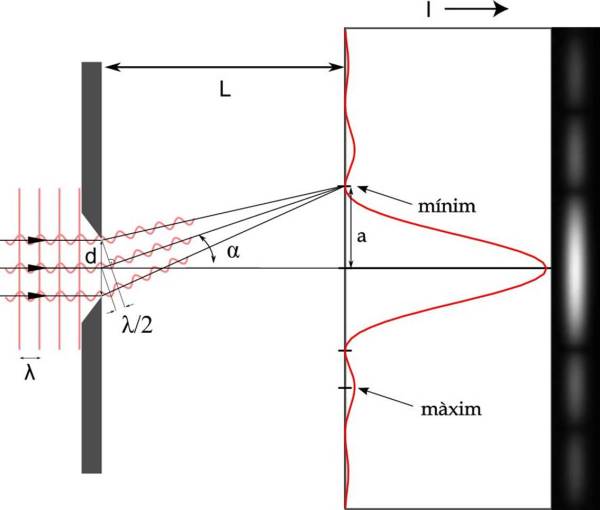
L’equació que relaciona les magnituds implicades per a calcular on es troba la primera zona fosca a banda i banda del màxim central, si es considera que la distància de la pantalla a la ranura és molt més gran que la seva amplada, ha de ser
λ =d· a/L
i en general
m·λ = d·a/L, on m = 1, 2, 3,…..
D’altra banda, si la llum de la vora inferior es troba una longitud d’ona i mig al davant (3/2), un terç del feix no interferirà de forma destructiva amb la resta i es podrà apreciar un primer màxim al patró de difracció. La fórmula per trobar els màxims és una mica més complexa que pels mínims, aproximadament (2m + 1) λ/2 = d·a/L, on m = 1, 2, 3…i m=1 correspon a les primeres franges lluminoses a totes dues bandes del centre.

La fotografia de dalt està feta amb les condicions que indico al seu peu. A ull nu s’aprecien les dues primeres zones fosques a banda i banda del centre a 1,4 cm però no he aconseguit una foto en la que es vegi clarament fosc aquest punt. Per a calcular aquesta primera distancia a la que tenim una zona fosca es millor mesurar la distància entre tres zones fosques a cada costat i després dividir-la per 6.
Obtenció d’escletxes simples

Igual que en el cas de les escletxes dobles o les xarxes de difracció, les simples es poden comprar a una casa de material escolar de laboratori o per internet en Amazon o Aliespress, però igualment es poden fer casolanament tallant un quadradet de paper d’alumini amb un cúter o dibuixant-les amb un programari de dibuix i imprimint-les en alta qualitat.
Una altra manera d’aconseguir una escletxa és utilitzar dues fulles d’afaitar antigues o dues targetes de plàstic opac i enfrontar les seves vores subjectant-les d’alguna manera que permeti que s’apropin o allunyin per tal d’aconseguir una amplada de ranura més o menys gran.
Difracció de la llum per una escletxa i principi d’incertesa de Heisenberg
Diversos autors proposen aprofitar aquest experiment de la difracció per una escletxa simple per a comprovar en un cas pràctic el principi d’incertesa de Heisenberg, com per exemple fan els professors Beltran Abrego, J. R. I col·legues (2013) de la Universidade Estadual paulista de Sao Jose do Rio Preto a Brasil a l’article Montagem de um conjunto experimental destinado a verificacao do princıpio da incerteza de Heisenberg.
Com ja hem comentat al principi d’aquesta entrada, el principi d’incertesa de Heisenberg estableix que les mesures simultànies del moment lineal i posició per a una partícula en moviment comporten una limitació en la precisió de cada mesura. És a dir, com més precisa és la mesura de la posició, més imprecisa és la mesura del moment lineal, i viceversa. En el cas més extrem, la precisió absoluta d’una variable implicaria una imprecisió absoluta respecte a l’altra. Si considerem un conjunt de fotons caracteritzats per la incertesa de la posició Δy i la incertesa del moment Δp, podem expressar la relació de Heisenberg com:
Δy·Δp ≥ h/4π
On h = 6,6262 ×10−34 J.s és la constant de Planck.
La incertesa de la posició Δy per a un grup de fotons que passen per una escletxa d’amplada d, podem considerar que sigui la pròpia amplada:
Δy = d
Per tal d’estimar Δp, suposem que els fotons que arriben a l’escletxa es mouen només en la direcció perpendicular a l’escletxa (direcció x), però després de passar per l’escletxa, tindran components de velocitat en ambdues direccions (x i y). La densitat de probabilitat per al component de velocitat del fotó en la direcció y, vy, vindrà donada per la distribució d’intensitat en el patró de difracció, i podrien reescriure el principi d’indeterminació com
Δy·Δpy ≈ h
Definint per α l’angle del primer mínim de difracció (Fig. Difracció per una escletxa simple), podem expressar la incertesa de la velocitat com:

Δvy = c sin α,
on c és la velocitat de la llum. La incertesa del moment lineal és, per tant,
Δpy = m·ΔVy =m·c·sin α
on m és la massa del fotó i c és la velocitat de la llum. El moment i la longitud d’ona d’una partícula estan vinculats a través de la relació de de Broglie: p = m·c = h/λ. Per tant,
Δpy = (h·sin α)/λ
Ja hem vist que en el cas d’una ranura simple el sinus de l’angle α del primer mínim de difracció per a angles prou petits és,
sin α = a/L,
i per tant,
Δpy = h·a/λ·L
Si ara substituïm a la relació d’incertesa els valors de Δy i Δpy que hem deduït ens queda:
h = Δy.Δpy = d·h·a/·L = d·h·a/λ·L
És a dir:
b·a/ λ·L = 1
Que és el que s’ha de comprovar. En el meu cas, substituint els valors aconseguits per a l’escletxa simple tenim:
53000 nm x 1,4 cm / 654 nm x 107 cm = 1,06 ≈ 1
com us volia mostrar.
Tres versions de l’acudit de Heisenberg
Heisenberg està fent un viatge per carretera i veu llums intermitents de policia al mirall del retrovisor. S’atura a un costat de la carretera i el mosso s’acosta al vehicle. Pregunta a Heisenberg: “Té alguna idea de com anava de ràpid?” “No, però estic força segur d’on estic”. Confós per aquesta resposta, el mosso diu: “Bé… anava a 70 en una zona de 50”. “Genial, ara estem perduts!” diu Heisenberg.
Sabeu per què diuen que la vida sexual de Heisenberg era tan dolenta? Perquè quan tenia l’energia no tenia el temps, i quan tenia el temps no tenia l’energia.
Sabeu per què diuen que Heisenberg va morir verge? Perquè quan trobava la posició no trobava el moment, i viceversa.


4t acudit ∆E∆t per anàlisi dimensional és equivalent a ∆p∆t -Pet què no es pot fer l.amor amb una química? -Pet què quan té l’Energia no troba el temps. Una abraçada, Marta
Moltes gràcies, Marta
Equivalent a ∆x∆p
[…] hem vist en una entrada anterior, Experiments de difracció en escletxes i Principi d’incertesa de Heisenberg, el fenomen de la difracció i la interferència de la llum a través de dues escletxes en el que […]
[…] hem vist en entrades anteriors alguns experimentes que es poden realitzar amb làsers tals com: Mesura de la longitud d’ona d’un làser amb una xarxa de difracció, Mesura de l’amplada d’una escletxa o del gruix d’un cabell, o L’experiment de la doble […]
[…] de la doble escletxa, tant referit a la llum com als electrons, la podeu trobar a Experiments de difracció en escletxes i Principi d’incertesa de Heisenberg […]