Un experiment a l’Any Internacional de la Ciència i la Tecnologia Quàntica 2025 (IYQ2025).

La llei d’Stefan-Boltzmann prediu que la potència total irradiada (P_R) per un objecte esfèric incandescent assimilable a un “cos negre” és:

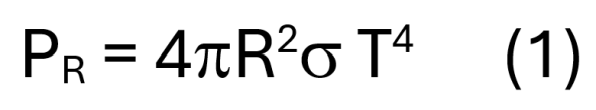
on T és la temperatura absoluta de l’objecte, R és el seu radi i σ és la constant d’Stefan-Boltzmann.

L’objectiu d’aquest experiment és comprovar que l’energia irradiada és proporcional a T⁴, amb un muntatge prou senzill, sent poc més que una petita bombeta incandescent.

Dos principis a considerar són:

1 La temperatura absoluta del filament de la bombeta és aproximadament proporcional en cada moment a la seva resistència. De manera que la temperatura i la resistència del filament estaria definida mitjançant la següent equació:

On T₀ és la temperatura ambient, R₀ la resistència en fred i n ≈ 1,2 en el cas del wolframi, encara que el calcularem després.

2 La potència elèctrica dissipada és la suma de la potència radiada (lluminositat) i la pèrdua de calor produïda, de manera que la potencia irradiada es pot calcular com la diferència entre la potencia consumida total i les pèrdues produïdes per conducció tèrmica a l’ambient. La llei del refredament de Newton suggereix que aquesta última serà proporcional a la diferència de temperatura amb l’entorn.

Procediment

El circuit seria com es mostra a sota. Qualsevol bombeta incandescent petita serveix. La font d’alimentació ha d’adaptar-se a la tensió de la bombeta i si no hi ha una font variable podeu utilitzar una pila i un potenciòmetre per variar la brillantor de la bombeta des de gairebé apagada fins a la seva tensió nominal o una mica més. Es pot utilitzar una bombeta de 3,5 V amb una pila de 4,5 V, encara que com que no tenia una pila a mà jo he utilitzat una font d’alimentació amb la sortida de 6 V i una bombeta de 4,8 V.

Dos polímetres barats també son suficients per apropar-nos a l’ordre de magnitud, però com al mesurar la intensitat s’han de posicionar en els 10 A per tal de no fer-los malbé, només ens proporcionen les centèsimes d’amper.

El mètode consisteix a començar a agafar mesures amb la bombeta inicialment apagada, i després augmentar gradualment la tensió d’alimentació fins a assolir la tensió màxima que suporti la bombeta.

En un full de càlcul es creen les columnes necessàries per introduir els valors del voltatge (V) aplicat a la bombeta i la intensitat que circula per ella (I) i, amb les fórmules adients, altres columnes per la resistència (R) i la potencia consumida total (Pt). Més endavant ja afegireu la potència perduda en forma de calor (Pc) i la potència irradiada (P_R).

Traceu la gràfica de la potència total contra la resistència (per tant, indirectament contra la temperatura). El gràfic comença com una línia recta però a temperatures més elevades augmenta la potencia més ràpidament, tal com es veu en color verd a continuació en el dibuix.

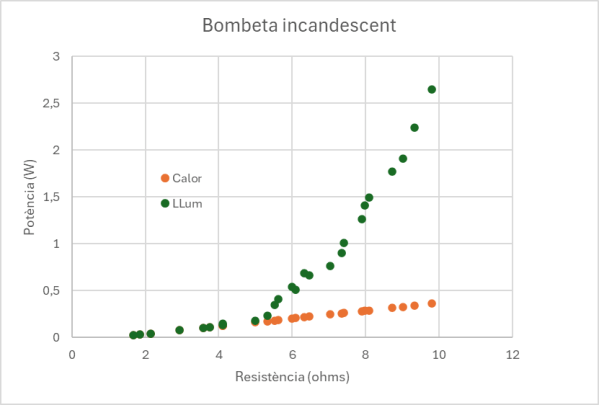
Si se selecciona només la part inicial recta del gràfic i s’afegeix una línia de tendència per aquests valors (que al gràfic apareix en color taronja), aquesta línia representa la pèrdua de calor a l’ambient deguda a la conducció. Aquesta potència perduda en forma de calor es calcula a parir de l’equació que subministra el full de càlcul de la línia de tendència de la part inicial quan encara no llueix la bombeta. A la taula de dalt ja hi és la columna amb la diferència entre la potència elèctrica total i aquesta pèrdua de calor, que representa la potència radiada P_R.

A diferència del que proposo aquí, la majoria dels autors utilitzen un fotodíode o una termopila per a mesurar la potencia irradiada per la bombeta. Per exemple, podeu mirar el protocol del Laboratorio virtual de Física Cuántica de la Universitat de València per estudiar la radiació d’un fill incandescent.

També Alejandro del Mazo i Santiago Velasco (2022), professors de l’IES Francisco Salinas i de la Universitat de Salmanca, respectivament, a l’article Medida de la constante de Planck con una lámpara de incandescencia y un led como fotodetector, de la Revista Eureka sobre enseñanza y divulgación de las ciències, expliquen com aconseguir experimentalment el valor de la constant de Planck gràcies a la llei d’Stefan-Boltzmann i a la mesura per un led verd de la llum emesa per la bombeta. Jo no he provat el protocol, però sembla tant fàcil de seguir com el que aquí proposo.

Continuem:

Com que P_R = k·T⁴ = k’·R^4/n, on k i k’ son constants, prenent logaritmes decimals:

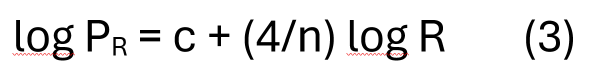
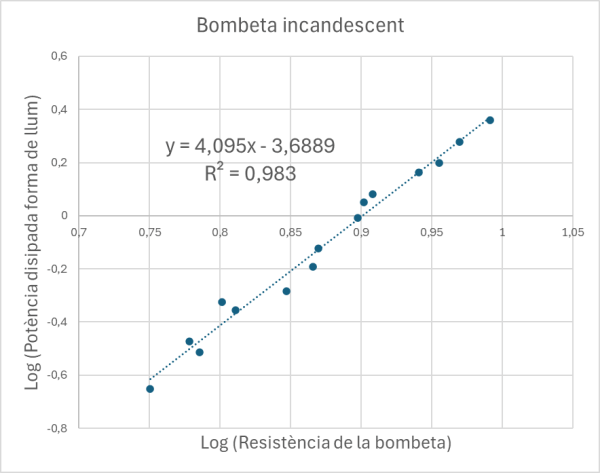
Ara s’ha de representar el logaritme de la potència irradiada en relació al logaritme de la resistència i ajustar els punts la millor línia recta. En aquest cas i en els següents ja només utilitzo els valors de la resistència per damunt dels 7 Ω, que corresponen a quan la bombeta ja està incandescent. El pendent de la línia hauria de ser aproximadament 4/n, demostrant així la forma de la llei d’Stefan-Boltzmann. En el meu cas el pendent és 4,095, que s’ha de multiplicar per n per obtenir el valor de l’exponent de la temperatura.

Per a calcular aproximadament el valor de n podem suposar que tota la potencia consumida per la bombeta és proporcional a la quarta potencia de la temperatura absoluta, i utilitzant les equacions (1) i (2) tindrem:

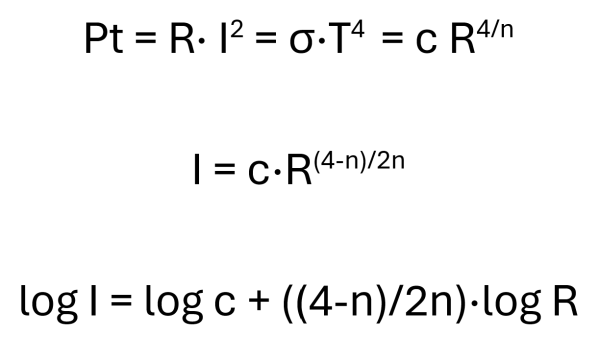
Si es dibuixa log I davant log R s’obté la gràfica següent, on la pendent (4-n)/2n és 1,296. D’aquí s’obté un valor n = 1,11, que aplicant-lo al càlcul anterior dona un valor de l’exponent de la temperatura en la llei d’Stefan-Boltzmann de 4,5.

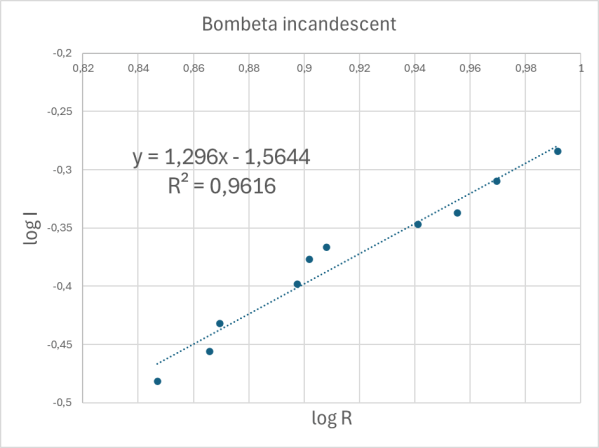
A la pràctica està molt bé obtenir un valor al voltant del 4, ja que tot i cometre en aquest cas una errada del 12,5 % crec que el valor és impressionant atès que s’investiga una llei complexa que involucra temperatures de fins a uns 3000K i per altra banda que permet discutir amb l’alumnat sobre estratègies i conceptes molt interessants, i tot amb uns mitjans del més senzill.

Aquesta llei a la que acabem d’apropar-nos inclou una constant de proporcionalitat, σ, que podem intentar obtenir amb el mateix disseny experimental que ja hem utilitzat, només canviant la bombeta per una més grossa en la que sigui visible amb facilitat el seu filament per a poder mesurar les seves dimensions, com per exemple les bombetes de 12 V i 21 W de els equips d’òptica d’Enosa/TSD. Per a fer els càlculs es necessita conèixer a més el radi del filament de la bombeta i la seva resistivitat (la del wolframi), tal i com explica el professor Luis A. Ladino en Determinación de la constante de Stefan-Boltzmann.

---